哥德巴赫猜想 x AICoder

唠唠闲话

上篇介绍了数学的后严谨阶段：直觉得到了严谨理论的坚实支撑，用于更准确地把握“大局观”。

本文通过例子展示直觉与问题把握如何相辅相成。为了便于入门，我们从俗易懂、前置知识要求较低的数论问题切入。

如果对更专业的例子感兴趣，可以参考：Weyl 群扩张群的结构 | SageMath 实战

在数学研究领域，计算推导是不可或缺的一环。从上世纪 60 年代开始，数学家就开始使用计算机辅助发现模式和猜想。如今，专业的数学编程语言，如 Mathematica，Maple，SageMath，GAP4 等，应运而生，极大地拓展了人类的计算能力。这些语言使我们能够完成传统手算难以实现的任务。在 LLM 快速发展的时代，编程任务可以通过 AI 辅助更轻松地完成。我们将在无需自己编写代码的情况下，借助 LLMCoder 来辅助对问题的探索思考。

哥德巴赫猜想

哥德巴赫猜想（Goldbach’s conjecture）是数论的经典问题，由德国数学家哥德巴赫于 1742 年提出，其内容是：

任何一个大于 2 的偶数都可以表示成两个素数之和

或者用严谨的数学语言表述：

$$2k=p+q,\ where\ p,q\in \mathbb{P},\ k\in \mathbb{Z}_{>1}$$

其中 $\mathbb{P}$ 表示素数集合。

数学家陈景润完成了 “1+2” 的证明，也即

$$2k=p_1 + q_1 \times q_2$$

其中

$$p_1,q_1\in \mathbb{P} ,q_2\in \mathbb{P}\cup\{1\},\ k\in \mathbb{Z}_{>1}$$

以下摘自本科的笔记。通过对问题的思考发散，从其他角度加深对这一猜想的认识理解，同时探索与之相关的规律现象。

思考发散

出于对经典问题的敬畏，这类问题必然被专业研究过，不建议花时间深入，否则容易成为下一个民科。

探究模式：

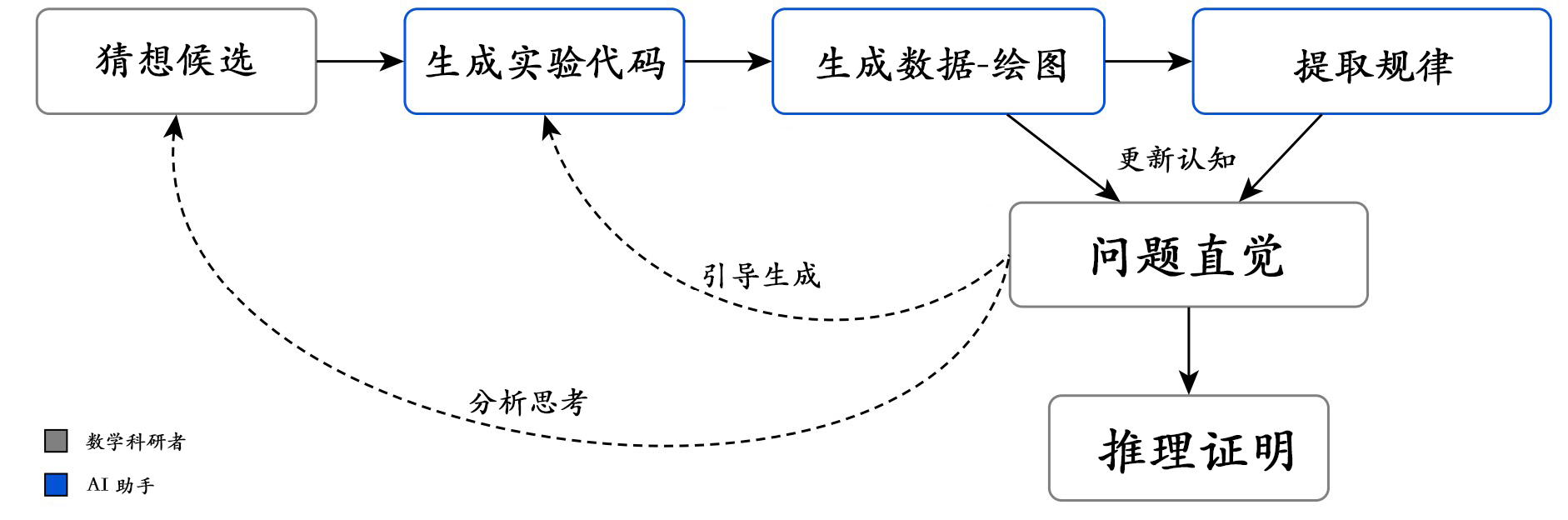
通过编程寻找规律，并基于发现不断修正思考，往复迭代。

思考 1

注意到偶数在分解时，可能存在多种方式，比如

$$40=3+37=11+29=17+23$$

这表明哥德巴赫猜想中的素数集可能存在冗余。因此：

思考1：是否存在素数的极小真子集 $S\subsetneqq \mathbb{P}$，使得猜想仍然成立，即

$$2k=p+q,\ where\ p,q\in S\subsetneqq \mathbb{P},\ k\in \mathbb{Z}_{>1}$$

这里“极小”指如果从 $S$ 中去掉任意一个元素，则上述命题将不成立。

特别地，这些极小真子集 $\{S\}$ 在字典序中最大和最小的情形分别是什么样子？通过观察精炼的子集，或许能够发现其他有趣的模式和规律。

思考 2

关于真子集的构造，介绍一种思路。

注意到，当 2k 较大时，分解不需要很小的素数，比如根据 $40=17+24$，将 40 分解为两素数和只需要用 $\{p\geq 17 | p\in \mathbb{P}\}$ 的素数。

定义函数 $f_0(k)$ 为偶数 $2k$ 是所有分解中“最大素数对”的较小值，对于前边例子有 $f_0(20)=17$。严谨的数学定义为：

$$f_0(k):=\max\{\min(p,q) | 2k=p+q,\ p,q\in \mathbb{P}\}$$

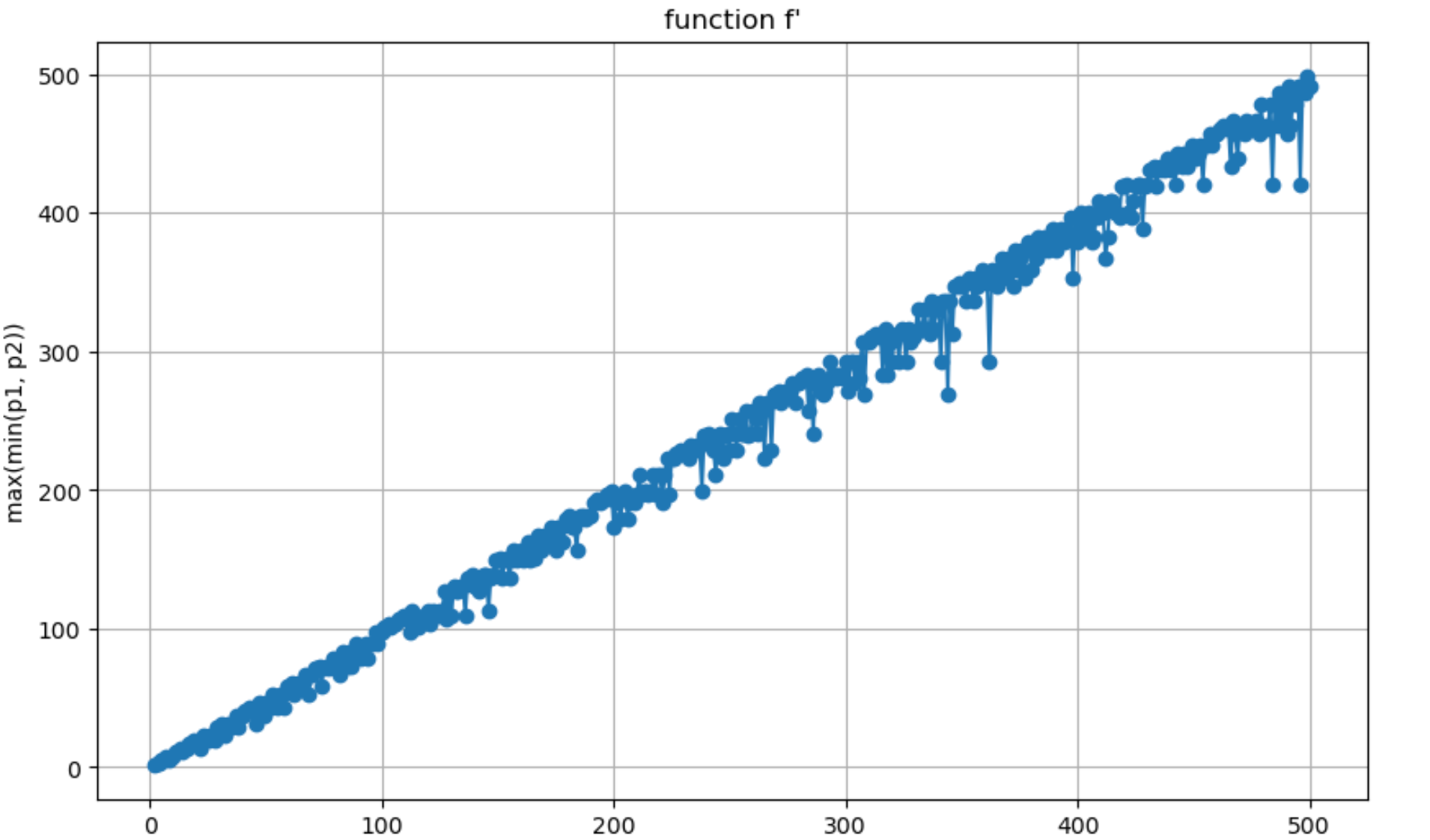
于是，偶数 2k 的分解只需用到 $\{p\geq f_0(k) | p\in \mathbb{P}\}$ 的素数。特别地，基于 $f_0$ 定义函数 $f$：

$$f(n) := \min\{ f_0(k) | k \geq n\}, \ n\in \mathbb{Z}_{>1}$$

换言之，对于大于等于 $2n$ 的偶数，分解只需使用 $\{p\geq f(n) | p\in \mathbb{P}\}$ 的素数。

因此，对于给定整数 $N$，可以将大于 $2$ 的偶数集分成两部分：

$$\{2n |n \leq N,\ n\in \mathbb{Z}_{>1}\} \cup \{2n |n > N,\ n\in \mathbb{Z}_{>1}\}$$

其中，较大偶数的分解只用到 $\{p\geq f(N) | p\in \mathbb{P}\}$ 的素数。因此只要分解较小偶数时，能不使用集合 $\{p < f(N) | p\in \mathbb{P}\}$ 的某些素数，那么这些素数就可以被剔除。

当然，这个思路有个潜在问题。我们不确定 $f(N)$ 是否随 $N$ 的增大而增大，也即，如果存在某些大偶数，分解必须用到很小的素数，那么这个思路就不可行了。

由于不确定这个想法是否可靠，可以通过计算和分析多个例子来检验。借助编程，可以迅速在大规模数据上验证，极大拓宽了获得数学直觉的途径。

补充

特别强调一点，统计规律不等于数学证明，编程实验可以揭示可能的方向，激发数学直觉，但不能替代证明。

举个低阶成立但高阶错误的经典例子。下表是前 12 阶的例子，容易发现，所有多项式的系数都是 0 或 $\pm 1$，而且一直算到 104 阶都是如此。

$$\begin{array}{|c|c|c|c|} \hline n & f(x) & n & f(x) \\ \hline 1 & x-1 & 7 & x^6+\cdots+x+1 \\ 2 & x+1 & 8 & x^4+1 \\ 3 & x^2+x+1 & 9 & x^6+x^3+1 \\ 4 & x^2+1 & 10 & x^4-x^3+x^2-x+1 \\ 5 & x^4+\cdots +x+1 & 11 & x^{10}+\cdots+x+1 \\ 6 & x^2-x+1 & 12 & x^4-x^2+1 \\ \hline \end{array}$$

注：分圆多项式是指多项式 $x^n-1$ 分解因式结果中的一个特定多项式 $f(x)$，满足 $f(x)=0$ 的解都不是低于 $n$ 次的形如 $x^n-1=0$ 的方程的解。

但第 105 阶的分圆多项式系数出现了 -2，从而打破了之前的规律。如果依赖手算，除非基于经验先检查特殊情况（比如 105=357），否则很难发现错误。

编程计算能有效规避一些低级错误。比如探讨群的换位子集与换位子群是否恒等时，最小反例要 96 阶。但群的同构类难以手工推算，此时必须借助专业的数学软件才能找到反例。

LLMCoder

整理对话历史(TODO)：

https://shared-chats.cubenlp.com/prime.html

AI Guided Intuition

Deepmind 的工作。(TODO)

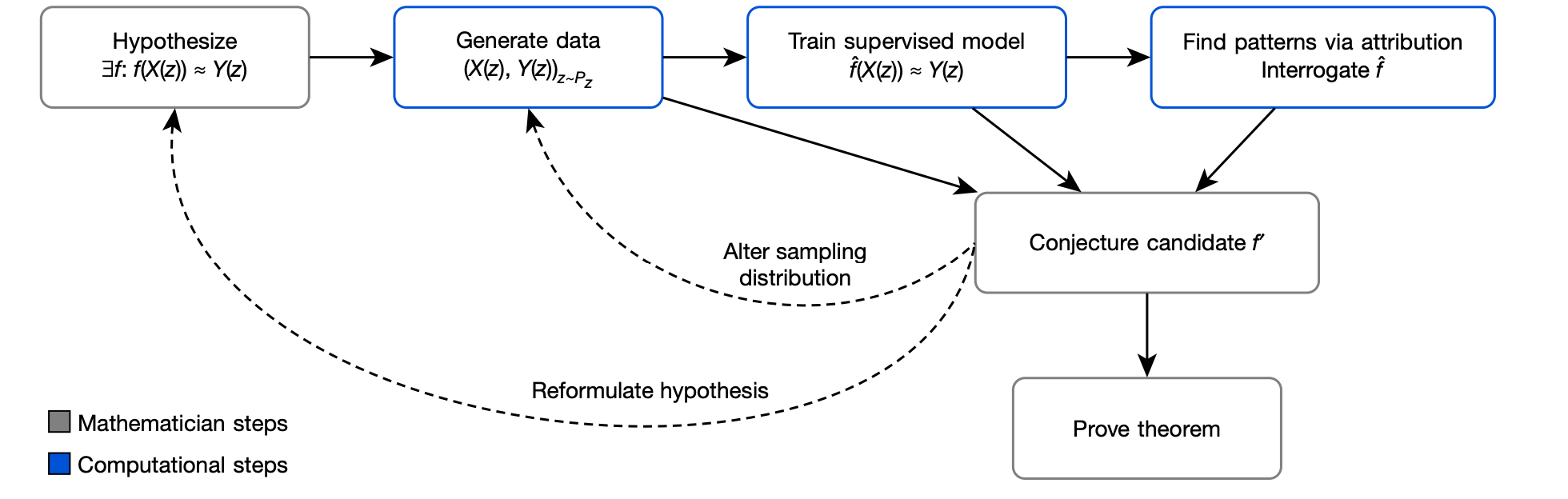
总结

就像上一篇短文提到的，形式化可以帮助我们避免常见错误并消除误区；编程实验同样能够发挥类似的作用，协助避免潜在的错误并修正对问题的直觉。

虽然编程往往只能展示规律，但它在引导数学直觉方面颇具价值。另外，也有一些问题用穷举能直接解决，比如四色定理，或用 SageMath 演示的另一个例子。

以上，演示数学问题 + LLM 的研究过程。