AI 改写数学竞赛 | 从 IMO Grand 到 AlphaProof

发表于 更新于 阅读次数： 字数： 4.4k 时间 ≈ 16 分钟
数学竞赛大致分为两类：一类面向高中生，例如国际数学奥林匹克竞赛（IMO）及相关选拔赛；另一类涵盖本科以上知识，如全国大学生数学竞赛和阿里巴巴数学竞赛等。IMO 作为高中生数学竞赛的巅峰赛事，由于背景知识需求相对较少，成为了测评 AI 能力的绝佳试金石。

唠唠闲话

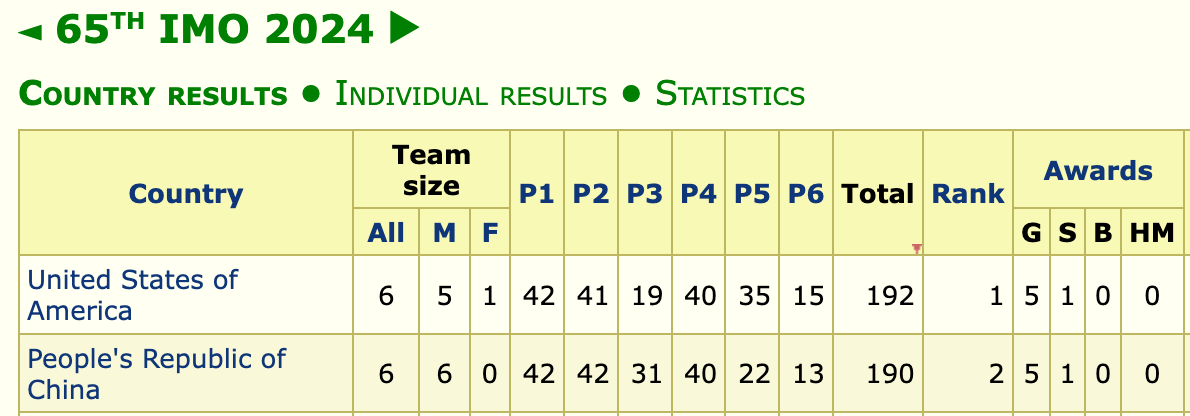
2024年7月21日，第 65 届 IMO 竞赛在英国巴斯落下帷幕。团体成绩方面，中国队以总分 190 分获得团体第二，结束了此前的“五连冠”，以 2 分之差惜败于美国队。

20240906202344

数学是人工智能的终极挑战，而数学竞赛是当前 AI 研究的热点之一。

今年7月初， Project-Numina 在 AI-MO 竞赛上获得了 29/50 的通过率；7月下旬，DeepMind 推出 AlphaProof 和 AlphaGeometry2，取得了 IMO2024 的银牌表现；9月中旬， OpenAI 的 o1 模型在 “IMO 资格赛” 上获得 83% 的准确率。

研究 AI 与数学竞赛有很多优势：

  • 问题答案明确，利于机器判分
  • 题目每年更新，持续提供挑战
  • 竞赛评分标准能让 AI 系统与人类选手直接比较

数竞按知识范围分两类：一类面向高中生，例如国际数学奥林匹克竞赛（IMO）及相关选拔赛；另一类涵盖本科以上知识，如全国大学生数学竞赛，丘成桐数学竞赛，阿里巴巴数学竞赛和 PutNam 竞赛等。而 IMO 作为高中生数学竞赛的巅峰赛事，因知识需求较少，成为了测评 AI 能力的绝佳试金石。

本文聚焦于前者，即国际数学奥林匹克竞赛（IMO）以及 AI 与这类竞赛的结合。

内容概要：

  • 第一部分介绍 IMO 的背景、考察范围、评分形式、相关选拔赛及赛题资源。
  • 第二部分介绍 AI 在数学竞赛领域的研究进展，从 2020 年的 IMO Grand Challenge 到今年的 AI-MO 竞赛，以及 DeepMind 的 AlphaProof 等。

IMO 竞赛

竞赛简介

国际数学奥林匹克竞赛（IMO，International Mathematical Olympiad）是专为高中生设立的全球性数学竞赛，也是所有国际科学奥林匹克竞赛中历史最悠久的一项。自 1959 年在罗马尼亚举行首届比赛以来，除 1980 年外，IMO 每年如期举行，现已成为全球最负盛名的数学竞赛之一。各参赛国派出最多六名学生组成的代表队，并配备一名领队、一名副领队及若干观察员。

竞赛内容涵盖复杂的代数、初级微积分，以及其他在中学课程中不常见的数学分支，如投影几何、复数几何、函数方程、组合数学和数论等问题。IMO 的核心理念之一是，即便解答需要深入的数学功底，任何具备基本数学理解力的人都能理解题目。 这种理念促使题目设计者在看似简单的题目中融入精巧构造，往往只有极具创造力的参赛者才能获得满分。

考试及评分

尽管 IMO 没有官方大纲，但题目严格限制在高中数学范畴内，不涉及大学水平内容。题目通常分为几何、代数、数论和组合四大类，难度极高，要求选手具备高度的逻辑推理能力、丰富的数学素养和扎实的基础知识。

每个参赛国可以向主办国提交推荐题目(long list)，这些题目经过筛选形成候选题列表（short list），由 IMO 评审团最终挑选出六道题。题目通常按难度递增排列，Q1 至 Q6 两天内完成，选手每天解答三道题，每天限时 4.5 小时。为了确保公平，所有参赛国的领队在比赛开始前几天便会拿到题目，并与外界隔离，直到竞赛结束。

选手的分数由该国领队和副领队与主办国指定的协调员共同商定，最终由首席协调员确认。若出现争议且无法解决，则由评审团作出最终裁定。

选拔赛

各国的选拔流程各不相同，但通常包括一系列淘汰赛。参赛者必须未满 20 岁，且不得在任何高等教育机构注册。在此前提下，个人可以多次参加 IMO。每年每个国家仅有 6 名中学生代表出战 IMO，这些数学最强大脑经过层层筛选，一路披荆斩棘，过五关斩六将，才有能力进入国家队。

在中国，通过中国数学奥林匹克（CMO）选拔全国前 60 名选手组成国家集训队，最终挑选 6 名队员参加 IMO。选拔过程包括几个阶段：

  • 全国高中数学联赛（预赛）：按省级联赛排名，分省一、二、三等奖。一个省上万人参加高联，五六十个省一，0.5% 的晋升率。
  • 全国中学生数学冬令营（决赛）：省一等奖的前几名进入省队，每年全国约有 350 名参赛者入围决赛。
  • 国家集训队选拔：两轮选拔，60 进 15, 15 进 6。

在美国，选拔通过一系列逐步递进的比赛完成：

  • 美国数学竞赛（AMC, American Mathematics Competitions）：比赛分为 8、10、12 三个年级，考试为 25 道多项选择题。学生可选择参加 A 或 B 两场考试，并以最好成绩获得后续资格。
  • 美国数学邀请赛（AIME, American Invitational Mathematics Examination）：名列 AMC12 的前5% 或 AMC10 的前 2.5% 的学生可参加这项考试，答题时间为 3 小时，包含 15 道问题，难度逐渐增加，答案是 0 到 999 之间的整数。
  • 美国数学奥林匹克（USAMO, United States of America Mathematical Olympiad）：AMC 和 AIME 的成绩综合后，前 400 名左右的学生可参加这项 IMO 的“模拟赛”（对应中国的数学冬令营）。

目前形式化领域中常用的 MiniF2F 基准，题目大多来源于这些竞赛。例如：

  • amc12a_2019_p21 表示 2019 年 AMC 12A 第 21 题
  • aimeII_2020_p6 表示 2020 年 AIME II 第 6 题
  • imo_1964_p1_2 表示 1964 年 IMO 第 1 题的第 2 小题

推荐一部关于 IMO 选拔的纪录片，《美丽青年心灵》（Beautiful Young Minds），纪录了 2006 届英国队参加 IMO 的经历。本片同时致敬了以数学家纳什为原型的奥斯卡获奖电影《美丽心灵》（Beautiful Minds）。这里摘录片中一段饶有意思的对话：

20240910083035

显然，这类人有点不太寻常，他们喜欢生活在大多数人无法感知的精神世界里……大多数人甚至意识不到其存在，而数学就是这么一种精神世界。作为人类，与之接触，与之周旋互动，发现那些隐藏起来的美、微妙惊人的规律，探索这些神奇细节，确是一种荣幸。许多人会认为这是一种自我放纵，但实际上，这个精神世界是开启现代社会的钥匙。几乎所有你现在接触到的事物，本质上都源自于某种数学工程。

Clearly, there is something very unusual about people who enjoy inhabiting a mental universe that most poeple can’t see. Most people don’t know its there. And mathematical world is a mental world. But as human beings, its a priviledge to engage with it, to walk around it, to discover the beauties and astonishing patterns, and subtleties that lurk. It’s a remarkable world, and in some sense, many people would think of that as self-indulgent. Except that this unviverse has turned out to hold the key to controlling the modern world. Almost everything you touch now is essentially based on mathematical enigineering of some kind.

竞赛赛题

IMO 官方网站 提供历年真题、候选题和答案，从 1959 年至今的赛题资源，以及 2006 年至 2023 年的竞赛候选题。今年的竞赛候选题及答案将在明年 IMO 结束后公布。相关试题资源已整理在 Lean-zh/IMO_Resource。

此外，选拔赛的大部分题目都可以在 AoPS（Art of Problem Solving） 网站找到。

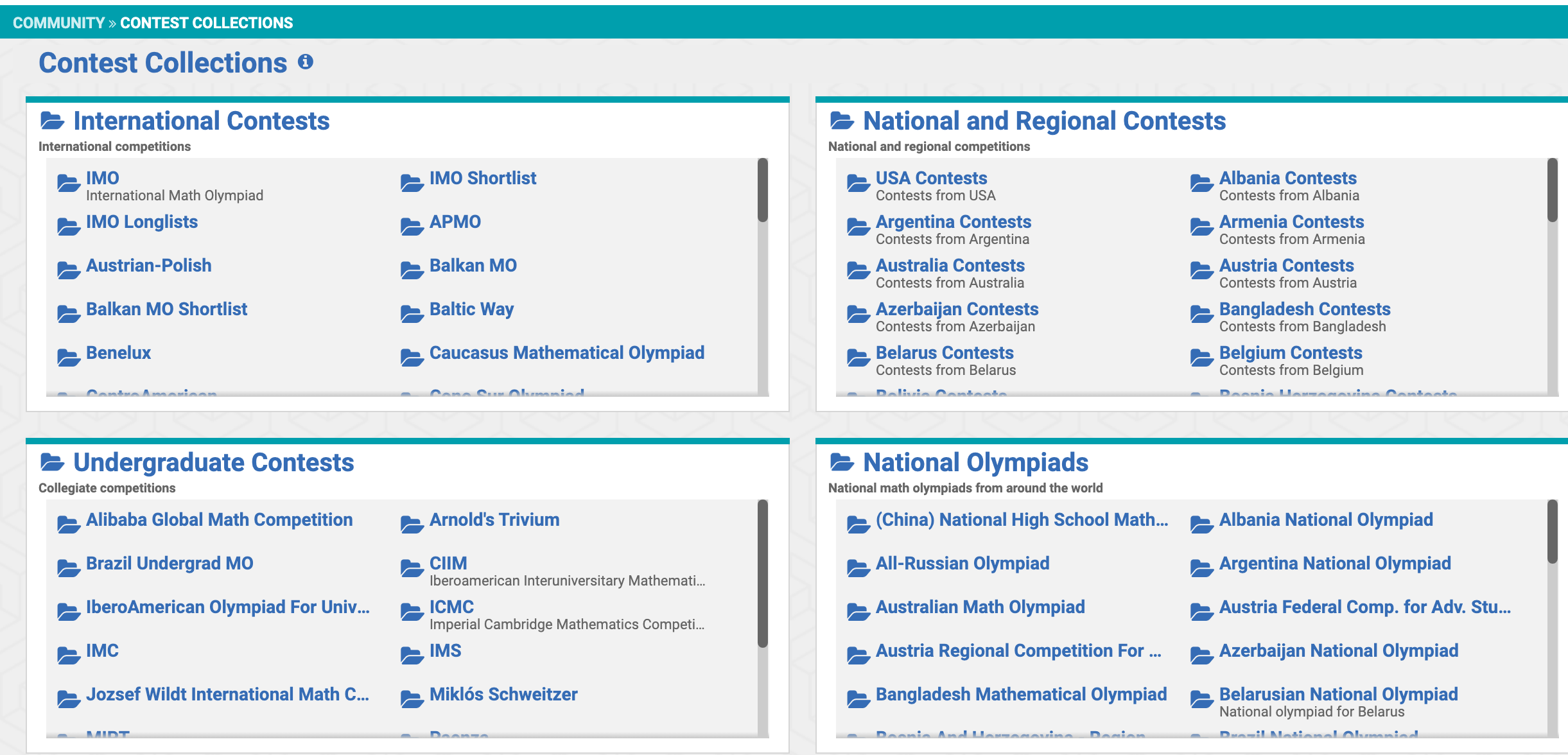
20240916104844

AoPS 是一个为数学爱好者打造的在线学习平台，聚集了一群喜欢钻研数学的学生。网站收集的资源覆盖了各个国家地区，不同层次的竞赛。同时提供一个热闹的社区，大家在这里讨论问题、分享解题技巧和经验。

总结

以上，第一部分我们介绍了 IMO 的背景、选拔流程和相关资源。接下来，将深入探讨 AI 在数学竞赛中的发展，探索 AI 如何面对这些极具挑战性的数学问题。

AI 与 IMO 竞赛

本节内容主要整理自 AITP 会议以及 Lean 社区相关的讨论。

AITP 与 LEAN 社区

自 2016 年以来，AITP（自动化定理证明）会议每年举办一届，与 IMO 相关报告包括：

此外，LEAN 的 Zulip 社区在数学形式化领域非常活跃，影响力大的工作都有相关讨论，比如今年的帖子：

  1. OpenAI o1 模型：OpenAI “Learning to Reason with LLMs”
  2. DeepMind IMO2024：IMO results from Google DeepMind
  3. AI-MO：AI Math Olympiad Prize
  4. 阿里巴巴数学竞赛 AI 赛道：Alibaba competition 2024 - AI track
  5. DeepSeek：DeepSeek-Prover 和 DeepSeek-Prover-V1.2
  6. IMO 频道：IMO Grand Challenge
  7. 机器学习与自动证明 频道：Machine Learning for Theorem Proving

欧式几何

IMO 竞赛的四大题型包括几何、数论、代数和组合数学。这里的几何特指欧式几何，相关工作包括：

  1. 上世纪 70 年代，吴文俊先生开创了机械定理证明，通过将几何问题代数化来实现自动定理证明。
  2. 2000 年，Shang-Ching Chou 提出的合成推理方法，开发了 Deduction database 系统。
  3. 2020 年，GeoLogic 由 Miroslav Olšák 开发，它是一个支持交互的逻辑核心系统，能够解决许多标准的高中几何问题。
  4. 2024 年初，DeepMind 的 AlphaGeometry 系统解决了 IMO 30 道题中的 25 道。最新版本的 AlphaGeometry2 进一步提升，能够解决过去 25 年间 83% 的 IMO 几何题。

注：欧式几何在现代数学的实际应用很有限，现代数学家更关注庞加莱猜想、微分流形，代数几何等更复杂更抽象的几何空间，这些更加考验数学家的想象力、理解能力与推理能力。

IMO Grand Challenge

IMO Grand Challenge 是微软研究院在 AITP 2020 上提出的重大挑战，旨在构建一个能够在 IMO 比赛中赢得金牌的人工智能系统。

规则与评分标准：

  1. F2F（Formal-to-Formal）：接收形式化的问题陈述，生成机器可检查的证明。
  2. 评分：证明须在 10 分钟内通过 Lean 核心的验证，这个时间约等于人类裁判审核人类解答的时间。证明没有部分得分，要么全对，要么全错。
  3. 资源限制：AI 参赛者拥有与人类相同的时间限制（每组三道题目需在 4.5 小时内完成），但可以使用无限的计算资源。
  4. 可复现性要求：AI 必须在比赛开始前开源，并允许公众访问和复现。在比赛期间，AI 不能访问互联网。

该挑战的组织委员会由来自 OpenAI、微软、谷歌等机构的研究者组成，包括：

  • Daniel Selsam（OpenAI）
  • Leonardo de Moura（微软研究院）
  • Kevin Buzzard（伦敦帝国理工学院）
  • Reid Barton（匹兹堡大学）
  • Percy Liang（斯坦福大学）
  • Sarah Loos（谷歌 AI）
  • Freek Wiedijk（奈梅亨大学）

2021 年 OpenAI 发布的 MiniF2F 基准与该挑战相关，以 F2F 的形式，扩展支持了更多的形式系统。

尽管 IMO Grand Challenge 为数学和 AI 社区提供了一个富有挑战性的任务，但遗憾的是，该项目目前并未设置奖项或表彰部分进展的机制。

AI-MO

2024 年 4 月，XTX Markets（一家金融科技公司）推出了人工智能数学奥林匹克奖（AI Math Olympiad Prize, AIMO），并设立了 1000 万美元的奖励基金，旨在推动开发一个能够在 IMO 中赢得金牌的公开共享的 AI 模型。

与 IMO Grand Challenge 的 F2F 模式不同，AIMO 采用的是 informal-to-informal 形式，赛题难度介于 AMC12 和 AIME 之间，每道题目的答案是 0 到 999 之间的整数，类似 AIME 的题目形式。

比赛内容：竞赛使用由专业题目设计团队创建的全新数据集，包含 110 道原创数学问题，难度从基础算术到高级代数和几何推理不等。题目被划分为三个部分：10 道“训练题”公开提供，50 道“测试题”用于评估提交质量（不公开），另有 50 道“验证题”决定最终排名（不公开）。这些问题都为原创，避免了数据泄露的风险。

评分形式：该竞赛在 Kaggle 平台上进行，详见 AI Mathematical Olympiad - Progress Prize 1。参赛者需使用官方提供的 Python API 进行评估，并按标准规范提交代码。

官方基准模型 Gemma 7B 在测试集和验证集上的通过率为 3/50。比赛的最佳成绩由 Numina 取得，该模型基于 DeepSeekMath-Base 7B 微调，结合自然语言与 Python REPL 解决数学问题，通过率达到 29/50。

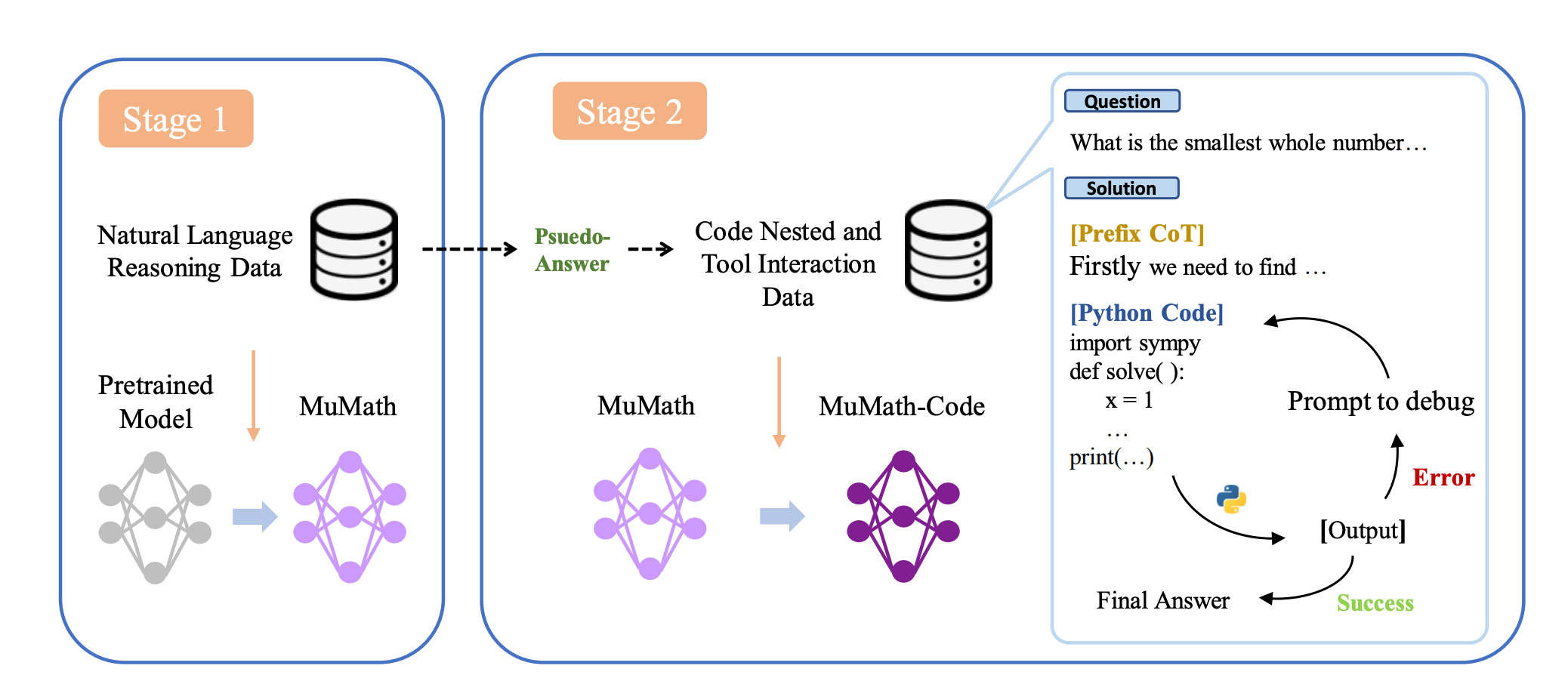
20240918112405

第一阶段微调得到中间模型，第二阶段用工具集成推理的合成数据集，将问题分解为一系列基本原理、Python 程序及其输出。

Project-Numina 开放共享了模型代码，模型参数，以及由 86 万条数学问题构成的数据集 AI-MO/NuminaMath-CoT。完整技术报告可在 Kaggle 的讨论区中找到。

此外，可以在 AI-MO 提供的在线模型服务体验 Numina 模型的效果：

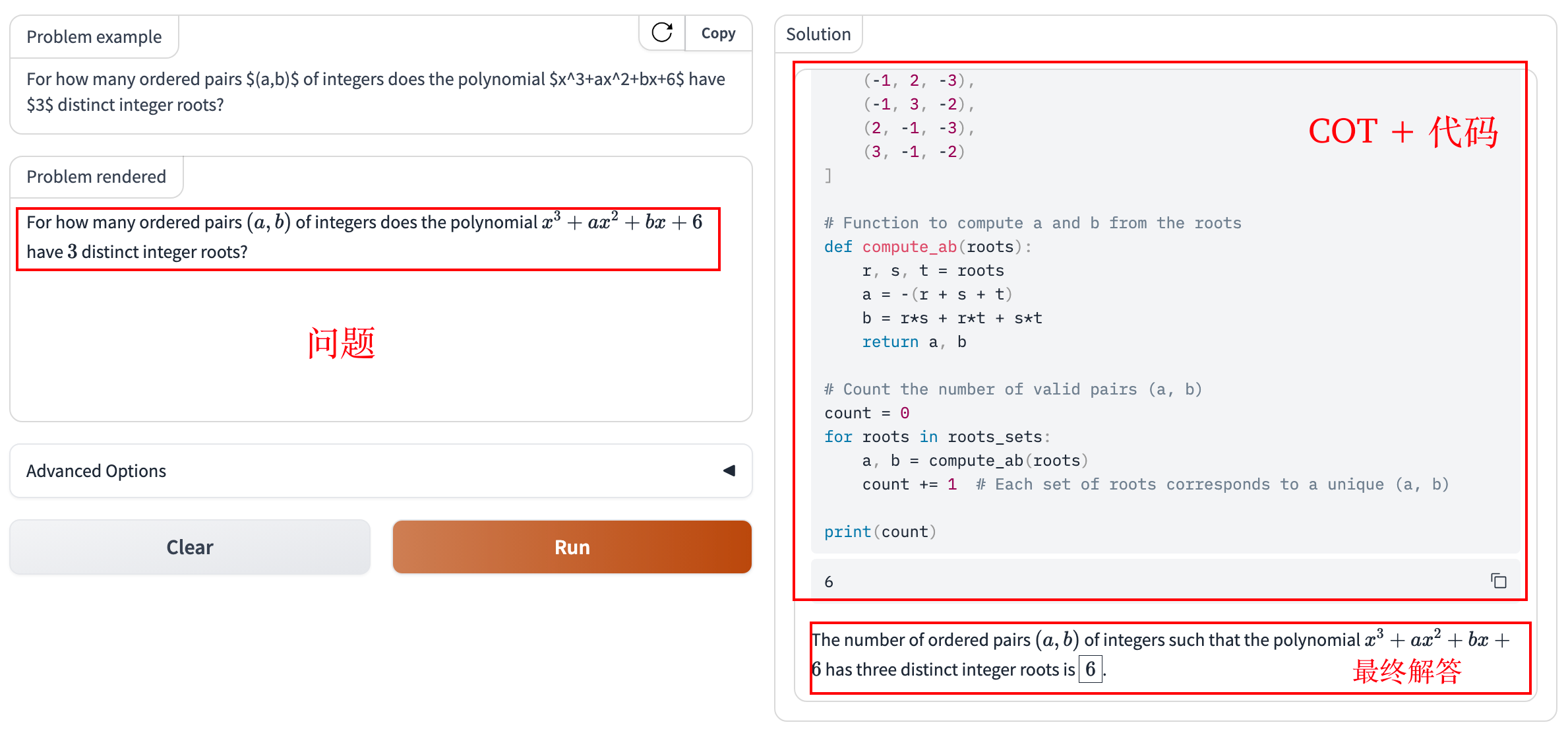
20240918223607

题解过程：COT + Python 代码 => 生成最后答案

注：该模型服务似乎下架了。

AlphaProof

与 AIMO 这类非形式化、只检验答案的竞赛不同，F2F（Formal-to-Formal）模式可能更能真正消除 AI 在数学推理中的幻觉。

比如前段时间大火的 OpenAI 的 o1 系列，其在 AIME 数据集上，从 GPT-4o 的 13% 准确率提升到 83%（cons@64），即使是 pass@1 的准确率也达到了 74.4%。

个人实测 o1-preivew 在 IMO2024 第一题的表现，相比于 GPT-4o，o1 模型在推理加持下确实能解答正确，但证明过程仍存在错误，关键步骤胡言乱语，蒙混过关。

https://www.zhihu.com/question/666992324/answer/3624340050

相比之下，DeepMind 的工作在推理证明方面更加出色。今年的 IMO 比赛结束后，DeepMind 推出了 AlphaProof，一种用于形式数学推理的强化学习系统；同时发布了 AlphaGeometry2，几何求解系统 AlphaGeometry 的改进版本。凭借这两个系统，DeepMind 成功解决了今年 IMO 六道题中的四道（p1、p2、p4、p6），这意味着 AI 首次达到了与银牌最高分相当的水平。

更具体地，AlphaProof 在几分钟内解决了一道题，随后花费了三天时间解决了另外两道；而 AlphaGeometry2 在收到形式化命题后的 19 秒内解决了第四题。

技术原理：数据合成 + 强化学习 + 搜索

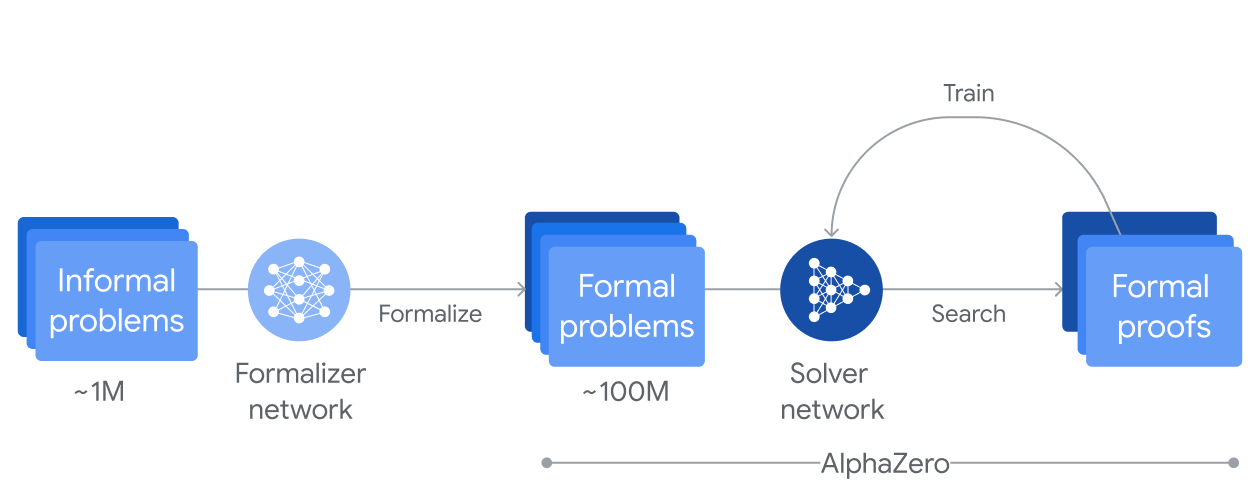
20240912053248

左侧：将大量非形式的数学问题通过“形式化网络”（微调的 Gemini 模型）翻译成形式数学语言。
右侧：使用“求解网络”来探索证明或反证，系统通过 AlphaZero 算法自我增强，从而能够解决越来越复杂的问题。每当系统找到一个新的证明，都会对模型进行强化，使其在处理后续问题时表现得更好。

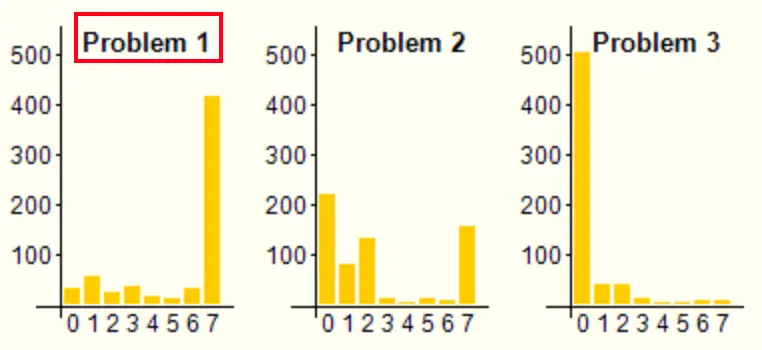
DeepMind 并未具体说明 AlphaProof 几分钟内解决的是哪一道题。从题目难度来看，p1 是一道人类几分钟内就能解决的简单题目，但 AlphaProof 在这道题上构造了繁复的证明，反而 p2 的证明相对简洁，因此可能 p2 对 AlphaProof 来说更容易。关于 IMO 2024 的详细题解分析，稍后我们将进一步展开讨论。

20240914151550

总结

以上，我们介绍了 IMO 及相关选拔赛，介绍了微软的 IMO Grand Challenge、XTX Markets 发起的 AIMO 竞赛，以及 DeepMind 的 AlphaProof 系统。相信在不久将来，我们就能见到 AI 在 IMO 竞赛中夺金，与人类顶尖数学家一较高下。

虽然目前的研究已取得显著成果，但在形式化推理和更加复杂的数学问题上，仍然有很大的探索空间。对于另一类面向更高知识水平的竞赛，有机会再开一期讨论~

20240918225250