AIMO 百万奖金赛 | Numina 技术原理解析

发表于 更新于 阅读次数： 字数： 3.1k 时间 ≈ 11 分钟
探讨了 Numina 在第二届 AIMO 竞赛中的技术方案，包括模型微调和推理算法。在数据集方面，Numina 开源了多个数据集用于模型的微调和验证，开放了微调各阶段的模型参数。Numina 取得最佳成绩的关键因素在于其**高质量的合成数据集**，其次是精心设计的微调技术和推理策略的选择。

唠唠闲话

第二届 AIMO 竞赛已在 Kaggle 上正式启动。

20241023211942

本次比赛的难度为国家奥赛级别，参赛者将面对 100 道全新数学题，要求 AI 展示真正的数学推理能力，而非简单的计算或猜测。本次进步奖的奖金池高达 209.7 万美元，比 2024 年 7 月颁发的首届进步奖翻了一倍。比赛于 10 月 17 日开始，将于 2025 年 4 月 1 日结束，历时 5 个月。参赛链接：

系列教程将逐步分析 AI + IMO 的相关工作，欢迎关注~

关于 AI-MO

AIMO 奖项设立于 2023 年 11 月，旨在推动能够胜任国际数学奥林匹克 (IMO) 水平的 AI 模型的研发。最终目标是创建一个能够赢得 IMO 金牌的 AI 模型，奖金为 500 万美元。此外，AIMO 还设立了一系列进步奖，以表彰实现这一目标的关键里程碑。

上一篇博文 AI 改写数学竞赛 | 从 IMO Grand 到 AlphaProof 我们详细介绍了 IMO 和相关选拔赛，以及 AlphaProof 等将 AI 应用于 IMO 的研究。本篇聚焦技术层面，回顾首届 AI-MO 竞赛的最佳工作 —— Numina，介绍其实现方案和技术细节。

Numina

Numina 于 2023 年底由一群热衷于人工智能与数学的研究者创立，包括 Jia Li、Yann Fleureau、Guillaume Lample、Stan Polu 和 Hélène Evain，得到了 Mistral AI 的初始支持。受到 AIMO 竞赛的启发，该项目专注于开发能够解决高难度数学问题的 AI 模型。

由于获奖队伍必须公开其代码、方法、数据和模型参数。作为第一届 AIMO 的获胜者，Numina 开源了完整的训练代码、数据集及微调后的模型参数，以及最终求解问题的代码，确保工作完全可复现。此外，Numina 还在 HuggingFace 平台上托管了一个在线运行的演示 Demo（不过该服务目前 404 了）。

技术解析

Numina 的技术方案由两部分组成：模型微调和模型推理。该团队在这两个方面进行了大量的尝试和探索。

模型微调

在微调方面，主要有以下三个关键要素：

  1. 模型基座的选择：以 DeepSeekMath-Base 7B 作为基座，通过全量微调，将模型转化为一个“推理代理”，能够利用自然语言推理和 Python REPL 来计算中间结果，从而解决复杂的数学问题。

  2. 工具集成推理解码算法 (TIR)：团队设计了一种创新的解码算法，用于整合工具以进行推理，并结合代码执行反馈，在推理过程中生成多个候选解答，从而提高解题的准确性。

  3. 内部验证集：为避免模型在公开排行榜上过拟合，Numina 创建了多组内部验证集，帮助指导模型的选择和优化。

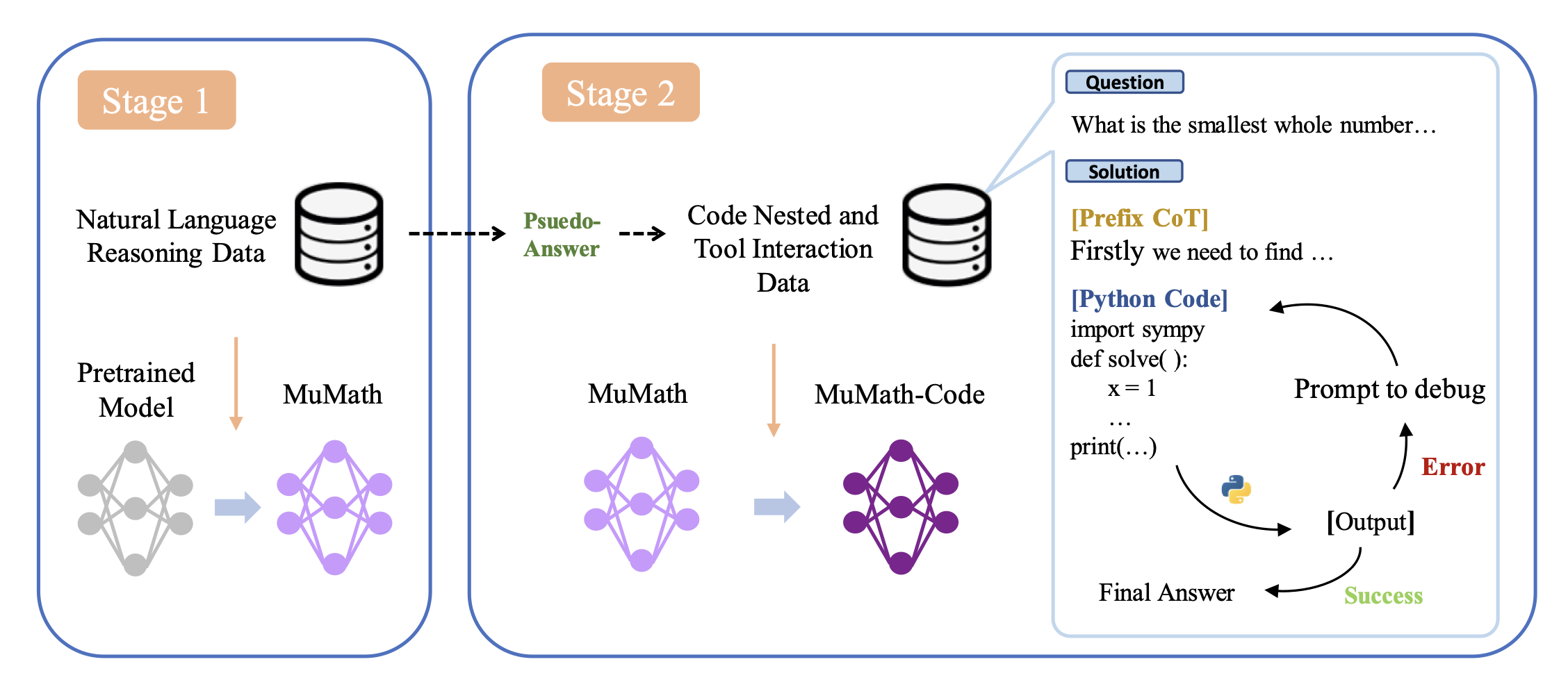
具体来说，微调过程依托 MuMath-Code 的研究，采用了两阶段训练法。工具集成则遵循 ToRA 的格式：

20241011035741

  • 第一阶段：采用 COT 模板构建的数据集 NuminaMath-CoT 对模型进行初步微调，从而提升模型的推理能力。

  • 第二阶段：基于 ToRA 方法，使用 GPT-4 生成具有代码执行反馈的 ToRA 格式解答，形成一个工具集成推理的合成数据集 NuminaMath-TIR。每个数学问题被解构为推理步骤、Python 代码及其输出，从而进一步微调模型。

其他技术细节：微调过程中，使用 TRL 的 SFTTrainer 的“打包”功能，将多个样本拼接在 2048 个 token 的块中进行处理。此外，通过梯度检查点和 DeepSpeed ZeRO-3 协议，实现了模型权重、梯度和优化器状态在有限显存中的高效分片。

推理算法

除了提升模型本身的性能，例如：采用更大的模型、构建更优质的数据集、选择更好的模型基座等；在固定模型的情况下，优化推理策略也能显著提升模型性能。比如：

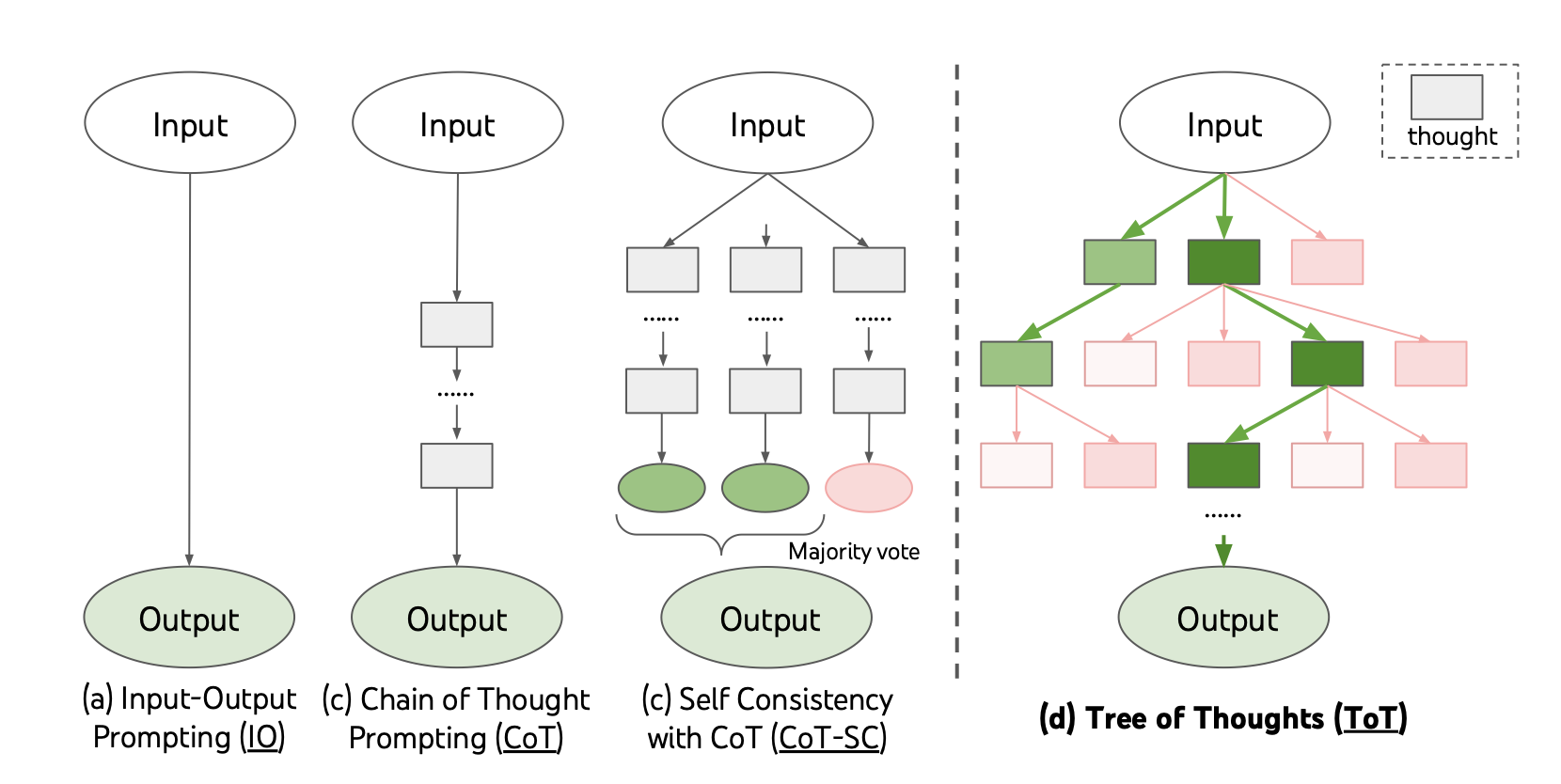
  • 使用多轮投票提高模型自一致性（Self-Consistency）
  • 集成外部工具的 TIR 策略
  • 使用双模型：策略模型 + 奖励模型
  • 使用 MCTs 树搜索算法选择最优分支

Numina 方案综合了前两个策略，形成 SC-TIR 算法：通过 Python 集成推理，并对生成的解答进行多数投票：

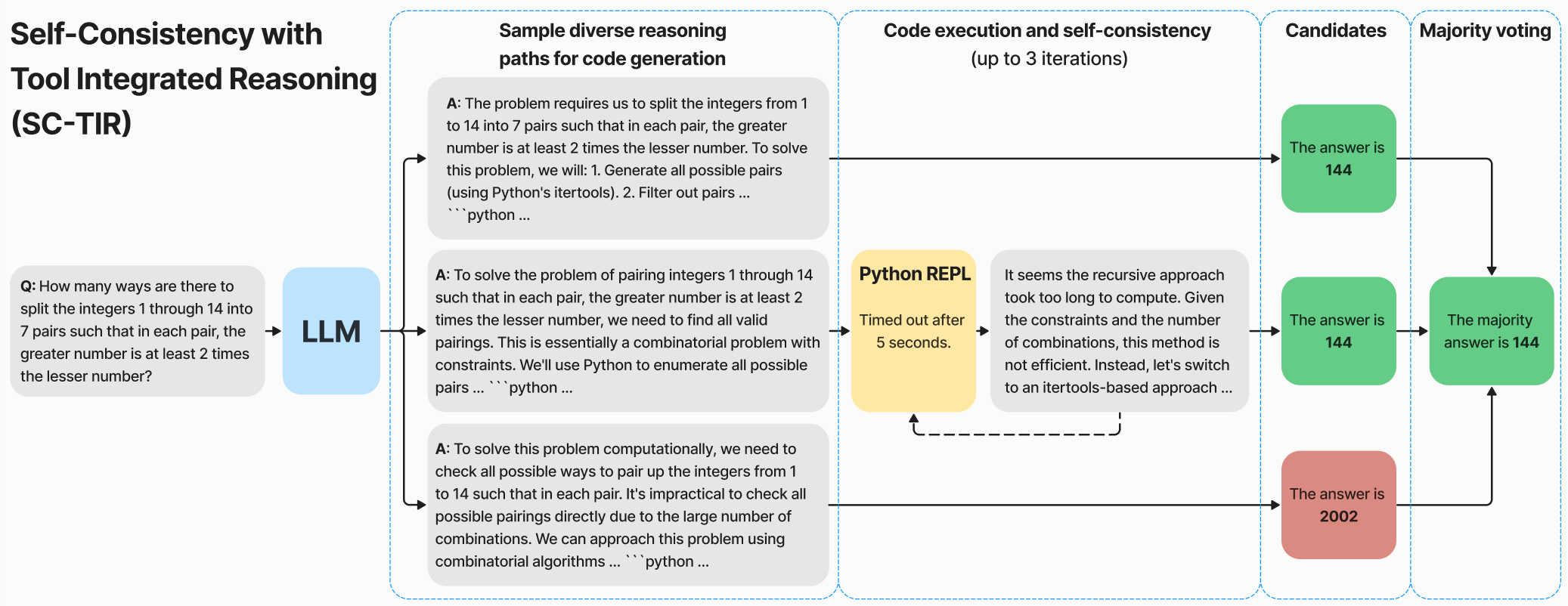
20241011014757

具体的算法步骤如下：

  1. 生成初始候选解：对于每个问题，将输入复制 N 次，作为 prompt 批次传送给 vLLM 模型，从而生成多个候选解以备多数投票。

  2. 多轮代码生成：模型通过采样生成 N 个多样化解答，持续运行生成完整的 Python 代码块，此过程可持续 M 轮以确保代码完整。

  3. 代码执行与反馈：执行生成的每个 Python 代码块，并返回输出及潜在错误信息（如 traceback），帮助模型发现并纠正错误。

  4. 推理轨迹创建：生成宽度为 N、深度为 M 的推理轨迹，让模型通过 traceback 反馈自我修正。如果某候选解无效（如代码不完整或执行失败），则其被修剪。

  5. 多数投票与后处理：在生成多个解答后，对候选解后处理，并通过多数投票选定最终答案，确保结果的可靠性和一致性。

简单说，就是多次代码生成与执行，以及多次采样并进行投票。

在这次竞赛中，前几名团队还采用了其他推理策略，后续再整理介绍。

20241011200939

实践摸索

在实现最佳解决方案之前，Numina 团队尝试了其他多种方法，以下是一些关键实验和结果：

  1. 纯 CoT 模型 + 多数投票：团队初期尝试了纯 COT 推理，并通过多数投票机制进行评估，取得了 8/50 的成绩。但这种方法未能展现出足够的解题能力。

  2. MMOS 数据集的应用：团队进一步尝试了使用 MMOS（Mix of Minimal Optimal Sets）数据集，将问题的解决过程简化为单轮 Python 程序的执行。这种方法提高了模型的表现，达到了 16/50 的成绩，但由于 MMOS 仅生成单轮解答，未能处理复杂的多步推理问题。

  3. KTO 优化方法：随后，团队转向了 Kahneman-Tversky Optimization (KTO) 算法。通过从 SFT 模型中每题抽取 4 个解答，与 Ground Truth 比较，生成正负样本，再对 SFT 模型应用 KTO 优化。此方法显著提高了模型表现，达到了 27/50 的成绩。此外，KTO 的一大优势是可以在训练过程中跟踪隐式奖励，帮助调试并优化模型选择。

  4. 其他模型的尝试：团队测试了多个更大规模的模型，包括 InternLM-20B、CodeLama-33B 和 Mixtral-8x7B，但这些模型在数学问题上表现都不如 DeepSeek 7B，且在推理时存在显著的延迟问题。

  5. RLOO 算法的尝试：使用 REINFORCE-leave-one-out (RLOO) 算法与 Proximal Policy Optimization (PPO) 进行强化学习，结合代码执行反馈与奖励机制进行训练。尽管在奖励曲线上看到了些许提升，但最终未能在整体表现上取得显著进步。

  6. 推理加速与模型合并：在推理加速方面，通过静态 KV 缓存与 torch 编译，可以在 H100 GPU 上将生成速度提升 2-3 倍，但在 Kaggle T4 环境中遇到了各种兼容性问题。团队还实验了多种模型合并技术（如 DARE、TIES 和 WARP），使用 mergekit 工具将 SFT 和 KTO 模型或公共 DeepSeekMath 模型合并。但这些尝试导致内部评估的显著退步，因此未进一步深入探索。

数据集和模型

当然，说到底，“Good data is all you need”。

Numina 数据集的来源广泛，包含中国的高中数学练习题、美国和国际数学奥林匹克竞赛（IMO）的问题等。大部分数据来自在线试卷的 PDF 文档和 AoPS 数学论坛。其中 AoPS 是一个国际化的数学论坛，也是 IMO 选手常用的资源。

数据处理流程：首先对原始 PDF 进行 OCR，然后将其分解为问题-解决方案对。接下来，将内容翻译成英文，进行调整以形成思维链推理格式，最后生成最终答案格式。

数据集

Numina 共开源了六个数据集：

  • 前两个数据集：基于搜集的问题，用 GPT-4 和 DeepSeek 进行标注。分别用于两个阶段的模型微调。
  • 后四个数据集：作为内部验证集，用于评估模型的泛化能力。团队利用这些验证集来衡量模型在不同难度数学问题上的表现，避免模型在基础数据上过度拟合。

数据集列表：

HuggingFace 地址 简述
AI-MO/NuminaMath-CoT 包含 86 万个数学问题及其 CoT 格式的解决方案
AI-MO/NuminaMath-TIR 从 CoT 数据集中选取 7 万个问题，由 GPT-4 生成的工具集成推理（ToRA）路径和代码
AI-MO/aimo-validation-aime 包含 AIME 2022-2024 年的 90 个问题及其解决方案
AI-MO/aimo-validation-amc 包含 AMC12 2022、2023 年的 83 个问题及其解决方案
AI-MO/aimo-validation-math-level-4 从 MATH 数据集中提取的 754 个 level 4 难度问题
AI-MO/aimo-validation-math-level-5 从 MATH 数据集中提取的 721 个 level 5 难度问题

除此之外，AIMO 官方的资源指南页面还提供了一些其他的资源来源，例如英国小学到高中的竞赛资源：

20241011053036

模型

Numina 团队基于 DeepSeek 和 Qwen 的基础模型进行了微调，形成了一系列适用于数学推理任务的模型。这些模型在不同阶段分别使用 CoT 和工具集成推理（TIR）数据集进行训练，并采用 AutoGPTQ 进行 8-bit 量化，从而提升推理效率。

模型列表：

HuggingFace 地址 简述
AI-MO/NuminaMath-7B-CoT 阶段 1 模型，使用 CoT 数据集对 deepseek-math-7b-base 进行微调
AI-MO/NuminaMath-7B-TIR 阶段 2 模型，使用 TIR 数据集对上一阶段模型进一步微调
AI-MO/NuminaMath-7B-TIR-GPTQ 最终模型，使用 AutoGPTQ 进行 8-bit 量化
AI-MO/NuminaMath-72B-CoT 使用 CoT 数据集对 Qwen/Qwen2-72B 模型进行微调
AI-MO/NuminaMath-72B-TIR 使用 TIR 数据集对 72B 模型进行进一步微调

总结

以上，我们探讨了 Numina 在第二届 AIMO 竞赛中的技术方案，包括模型微调和推理算法。在数据集方面，Numina 开源了多个数据集用于模型的微调和验证，开放了微调各阶段的模型参数。Numina 取得最佳成绩的关键因素在于其高质量的合成数据集，其次是精心设计的微调技术和推理策略的选择。