ICLR 2025 | 数学形式化工作速览

发表于 更新于 阅读次数： 字数： 38k 时间 ≈ 2:17
数学形式化的目的是提供一个**完全客观和可验证的证明过程**，使得任何了解该形式体系的人都能够检查证明的正确性，而不需要对证明本身进行主观判断。由于数学形式化能用于消除模型幻觉，在当下格外受到关注。

唠唠闲话

今年 ICLR 的论文开放审阅了，此次进入审阅共 11578 篇，其中很多数学主题的文章。特别地，我们重点关注形式化领域。

内容速览

数学形式化的目的是提供一个完全客观和可验证的证明过程，以便任何熟悉这种形式体系的人都可以核实证明的正确性，无需做出主观判断。形式化具备消除模型幻觉的潜力，因而在模型迅速发展的当下得到了特别的关注。

论文列表

通过对 Lean, Isabelle, miniF2F, ProofNet, autoformal 等词的检索筛选，找到了 20 篇形式证明相关的论文。除了 4-StepProof，6-SubgoalXL和9-ProD-RL 使用 Isabelle 语言外，其他都用了 Lean 语言。

序号 简写 标题及源文件
1 LeanAgent LeanAgent: 用于形式化定理证明的终身学习框架
2 ImProver ImProver：基于代理的自动证明优化
3 Herald Herald: 一个自然语言注释的 Lean 4 数据集
4 StepProof StepProof: 自然语言数学证明的逐步验证
5 Lean-STaR Lean-STaR: 学习交替思考与证明
6 SubgoalXL SubgoalXL: 基于子目标的专家学习定理证明方法
7 FormL4 过程驱动的 Lean 4 自动形式化
8 miniCTX miniCTX: 带有长上下文的神经定理证明
9 ProD-RL 通过奖励 LLMs 分层分解证明来进行形式定理证明
10 ProofRefiner 与大型语言模型协作证明定理：使用 ProofRefiner 增强形式化证明
11 Lean-ing “Lean” 于质量：高质量数据如何在自动形式化中胜过多语言多样性数据
12 Con-NF 重新思考并改进自动形式化：迈向忠实度指标和基于依赖检索的方法
13 FormalAlign FormalAlign: 用于自动形式化的自动化对齐评估
14 CARTS CARTS: 通过多样化策略校准和抗偏置树搜索推进神经定理证明
15 3D-Prover 3D-Prover：基于行列式点过程的多样性驱动定理证明
16 SynLean Lean 定理的合成生成
17 RMaxTS 利用证明助手反馈增强强化学习和蒙特卡洛树搜索
18 Alchemy 炼金术（Alchemy）：通过符号突变增强定理证明能力
19 ZIP-FIT ZIP-FIT：基于压缩对齐的无嵌入数据选择方法
20 LIPS 通过整合大型语言模型和符号推理来证明奥数不等式

一些其他形式化领域的研究工作：

  1. 一阶逻辑推理（FOL）：
  2. 可满足性问题求解（SAT）：Transformer Encoder Satisfiability: Complexity and Impact on Formal Reasoning
  3. 几何形式化：GeoX: Geometric Problem Solving Through Unified Formalized Vision-Language Pre-training

主题分类

我们从一些角度，对这些论文分类整合与介绍，目前只阅读了摘要和扫了文章，其中一些有价值且感兴趣的工作，再进一步展开。

整理可能存在疏漏，欢迎指正。

研究级数学

形式化在数学研究上有相当大的潜力，就像 IMO2024 陶哲轩报告说的，形式化可以消除人们对证明可靠性的疑虑，让数学家之间相互信任，并在未来开启新的合作模式。

目前，面向本科以上知识，用于研究级别问题的：

  • 1-LeanAgent：通过课程学习、动态数据库和渐进训练，持续提升定理证明能力，成功证明了人类未曾证明的162个定理，包括抽象代数和代数拓扑等领域的挑战性定理。
  • 2-ImProver：根据下游用途优化形式化证明，测试真实世界的本科、竞赛和研究级数学定理上的表现。
  • 3-Herald：利用 Mathlib4 语料库增强数据，能应用于研究生水平数学文献的自动形式化。

当然，还有一些涉及本科以上或研究级数学的文章也值得关注，尽管不是关于形式化的。比如数据集方面的 U-MATH, UGMathBench, MathOdyssey。其他像 Cayley Maze 用于解决魔方、排序和整数分解。

证明过程和自然性

除了能用，我们会更希望有用。这方面的尝试包括关注证明过程，以及强调与自然语言的对齐。

今年在结合自然语言，提升证明自然性，避免出现诡异证明的工作：

  • 3-Herald：一个自然语言注释的 Lean 4 数据集
  • 4-StepProof：将完整证明分解为多个子证明，实现句子级别的验证

强调过程

比较扎心的是，形式化解决问题，很少能直接搞定的（至少按我目前接触的认识）。但目前对于解决过程挺有用的，可能真正投入当前的使用。

模仿人类隐式的思考过程 5，
子目标 6，
编译器过程反馈 7，
强调先给有用的引理 8
强调主动生成引理 9。
强调协作用途，用于开发工具：10

其中第5个感觉很有意思，我们正常解题，除了最终写在纸上的，草稿也占了大部分，而且很多时候，整理过程会擦除我们思考的痕迹。

对于证明过程的强调

这里要回到对于什么是证明的思考，就像之前翻译的一篇工作：

  • 数学不仅仅是证明

如果把数学当成纯粹的游戏，那潜在的研究意义被大大削弱了。数学证明，除了增强人们对定理本身的信任，更希望能加深对问题的认识理解。

另一个例子是 AlphaProof 对 IMO2024 p1 的证明，左侧是 AlphaProof 暴露搜索的结果，右边是人类自然的解法。

to prove xxx, you need to prove yyy, to prove yyy, you need to prove zzz…
我觉得，除了关注能不能证明，更重要一点，你怎么证的。

列表里其他内容，也可做了大致的浏览：

自动形式化方面：

  • 自然语言解释 3, 4
  • Lean4 编译器反馈的过程驱动7
  • 数据合成 11
  • 双向等价+检索 12
  • 语义对齐 13。

强调策略的多样性：

  • 改进自动形式化 12
  • 抗偏置树搜索 + 多样性改进证明的 14
  • 用行列式点过程的过滤机制，生成多样性策略用于证明 15
  • 前向推理+元编程生成数据 16.
  • 其他关于证明策略的，在线强化学习改进蒙特卡洛树 17
  • 对 Mathlib 处理变形 18。

因为形式化语料的稀缺性，数据筛选策略 19 以及上边很多工作都涉及了合成数据。

数学竞赛相关 20。
非形式化的，竞赛相关的：Putnam，Omni, AoPS, SBSC, GeoILP。

数学形式化

接下来，我们对每篇工作的内容进行展开，翻译摘要并提炼其核心思想。

1. LeanAgent: 用于形式化定理证明的终身学习框架

基本信息

  • 论文地址：LeanAgent: Lifelong Learning for Formal Theorem Proving
  • 关键词：Theorem Proving, Formal Theorem Proving, Neural Theorem Proving, Lifelong Learning, Formal Mathematics, Large Language Models, LLMs, Curriculum Learning, Proof Search
  • 领域：neurosymbolic & hybrid AI systems (physics-informed, logic & formal reasoning, etc.)

核心内容：通过课程学习、动态数据库和渐进训练，持续提升定理证明能力，成功证明了人类未曾证明的162个定理，包括抽象代数和代数拓扑等领域的挑战性定理。

摘要

大型语言模型（LLMs）在与Lean等交互式证明助手结合方面，在数学推理任务如形式化定理证明中取得了成功。现有方法通常涉及在特定数据集上训练或微调LLM，以在特定领域（如本科水平数学）中表现良好。然而，这些方法在泛化到高级数学时遇到困难。一个根本性限制是这些方法在静态领域上操作，未能捕捉到数学家们常常跨多个领域和项目同时或循环工作的方式。本文提出了LeanAgent，这是一种新颖的终身学习框架，用于定理证明，能够持续泛化并改进不断扩展的数学知识，同时不忘却之前学到的知识。LeanAgent 引入了多项关键创新，包括一种优化数学难度学习轨迹的课程学习策略、用于高效管理演变中的数学知识的动态数据库，以及平衡稳定性和可塑性的渐进式训练。LeanAgent 成功证明了人类未曾证明的162个定理，涵盖23个不同的Lean存储库，许多来自高级数学领域。其表现比静态LLM基线高出最多11倍，证明了抽象代数和代数拓扑等领域的挑战性定理，同时展示了从基本概念到高级主题的清晰学习进展。此外，我们分析了LeanAgent在关键终身学习指标上的卓越表现。LeanAgent在稳定性和后向迁移方面取得了优异的分数，其中学习新任务提高了对先前学习任务的性能。这强调了LeanAgent的持续泛化能力和改进，解释了其卓越的定理证明性能。

2. ImProver：基于代理的自动证明优化

基本信息

  • 论文地址：ImProver: Agent-Based Automated Proof Optimization
  • 关键词：Automated Proof Optimization, Neural Theorem Proving, Formal Mathematics, Lean Theorem Prover, Proof Generation, Large Language Models, Symbolic Reasoning, Interactive Theorem Proving
  • 领域：neurosymbolic & hybrid AI systems (physics-informed, logic & formal reasoning, etc.)
  • TLDR: ImProver optimizes formal mathematical proofs for arbitrary metrics using LLM agents, automatically improving proof readability and length in Lean as well as generalizing NTP.

核心想法：根据下游用途优化形式化证明，测试真实世界的本科、竞赛和研究级数学定理上的表现。

摘要

大型语言模型（LLMs）已被用于在 Lean 等证明助手中生成立数学定理的形式化证明。然而，我们通常希望根据其下游用途优化形式化证明的各种标准。例如，我们可能希望证明遵循某种风格，或者具有可读性、简洁性或模块化结构。拥有适当优化的证明对于学习任务也很重要，特别是由于人工编写的证明可能并不适合该目的。为此，我们研究了一个新的自动证明优化问题：重写证明，使其正确并针对任意标准（如长度或可读性）进行优化。作为自动证明优化的第一种方法，我们提出了 ImProver，这是一个大型语言模型代理，它重写证明以在 Lean 中优化任意用户定义的指标。我们发现，简单地将 LLMs 应用于证明优化是不够的，因此我们在 ImProver 中融入了各种改进，例如在一种新颖的 Chain-of-States 技术中使用符号化的 Lean 上下文，以及错误纠正和检索。我们测试了 ImProver 在重写真实世界的本科、竞赛和研究级数学定理上的表现，发现 ImProver 能够重写证明，使其显著更短、更具模块化，并且更具可读性。

3. Herald: 一个自然语言注释的 Lean 4 数据集

基本信息

核心思想：Herald 数据集和翻译器，通过双重增强策略，并利用 Lean-jixia 系统翻译 Mathlib4 语料库，能应用于研究生水平数学文献的自动形式化。

摘要

可验证的形式语言如 Lean 对数学推理产生了深远影响，尤其是在使用大型语言模型（LLMs）进行自动推理方面。训练这些形式语言的 LLMs 面临的主要挑战之一是缺乏将自然语言与形式语言证明对齐的平行数据集。为解决这一问题，本文引入了一种新颖的框架，用于将 Mathlib4 语料库（一个统一的形式语言 Lean 4 的数学库）翻译成自然语言。在此基础上，采用一种双重增强策略，结合了基于策略和基于非正式的方法，并利用 Lean-jixia 系统（Lean 4 分析器）实现这一目标。我们展示了这一流程在 Mathlib4 上的结果，称为 Herald（基于层次和检索的翻译 Lean 数据集，Hierarchy and Retrieval-based Translated Lean Dataset）。我们还提出了 Herald 翻译器，该翻译器在 Herald 上进行了微调。Herald 翻译器在 miniF2F-test 中的形式化陈述上达到了 93.2% 的准确率（Pass@128），在我们内部研究生水平教科书数据集上达到了 22.5% 的准确率，优于 InternLM2-Math-Plus-7B（74.0% 和 7.5%）和 TheoremLlama（50.1% 和 4.0%）。此外，我们提出了一个面向实际应用的章节级翻译框架。作为 Herald 翻译器的直接应用，我们成功翻译了 Stack 项目中的一个模板章节，标志着在研究生水平数学文献自动形式化方面的重要进展。我们的模型及数据集将很快向公众开源。

4. StepProof: 自然语言数学证明的逐步验证

基本信息

核心思想：将完整证明分解为多个子证明，实现句子级别的验证。

摘要

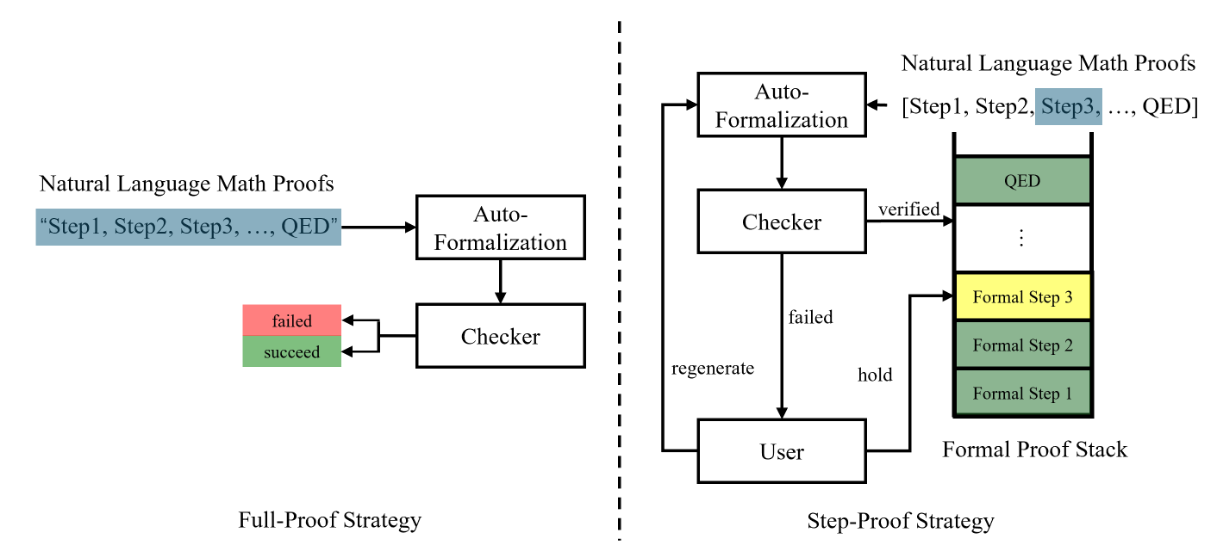
交互式定理证明器（ITPs）是强大的工具，能够对数学证明进行到公理层面的形式验证。然而，它们缺乏自然语言接口仍然是一个重大的限制。近年来，大型语言模型 (LLMs) 的发展增强了自然语言输入的理解能力，为自动形式化铺平了道路——将自然语言证明翻译成可以验证的正式证明的过程。尽管取得了这些进展，现有的自动形式化方法仅限于验证完整的证明，缺乏更细粒度、句子级别的验证能力。为了填补这一空白，我们提出了 StepProof，一种新颖的自动形式化方法，设计用于粒度、逐步验证。StepProof 将完整的证明分解为多个可验证的子证明，从而实现句子级别的验证。实验结果表明，与传统方法相比，StepProof 显著提高了证明成功率和效率。此外，我们发现对自然语言证明进行少量手动调整，使其更适合逐步验证，进一步增强了 StepProof 在自动形式化中的性能。

20241018093727

5. Lean-STaR: 学习交替思考与证明

基本信息

核心思想：Lean-STaR 框架，引入非正式思考过程并应用专家迭代。

摘要

传统的基于语言模型的定理证明，假设通过在足够多的形式化证明数据上进行训练，模型将学会证明定理。本文的关键观察是，大量在形式化证明中不存在的非正式信息对学习证明定理是有用的。例如，人类会思考证明的步骤，但这一思考过程在最终代码中是不可见的。本文提出了 Lean-STaR（Synthetic Thoughts Reasoning)框架，用于训练语言模型在每个证明步骤之前生成非正式的思考，从而提升模型的定理证明能力。Lean-STaR 使用回顾性真实策略生成合成思考来训练语言模型。在推理阶段，训练好的模型直接在预测每个证明步骤的策略之前生成思考。基于自学推理者框架，我们进一步应用专家迭代，在模型采样并使用Lean求解器验证的正确证明上微调模型。Lean-STaR显著优于基础模型（43.4% → 46.3%，Pass@64）。我们还分析了增强思考对定理证明过程各个方面的影响，提供了其有效性的见解。

6. SubgoalXL: 基于子目标的专家学习定理证明方法

基本信息

核心思想：结合子目标证明与专家学习，最大化数据效用和采用针对性指导进行复杂推理

摘要

形式化定理证明，作为数学与计算机科学的交叉领域，随着大型语言模型（LLMs）的发展而重新引起广泛关注。本文介绍了 SubgoalXL，一种新颖的方法，它将基于子目标的证明与专家学习相结合，以增强 LLMs 在 Isabelle 环境中进行形式化定理证明的能力。SubgoalXL 解决了两个关键挑战：专业数学和定理证明数据的稀缺性，以及 LLMs 在多步骤推理能力上的需求。通过优化数据效率和采用子目标级别的监督，SubgoalXL 从有限的人工生成证明中提取更丰富的信息。该框架将子目标导向的证明策略与专家学习系统相结合，迭代地优化形式化陈述、证明和子目标生成器。利用 Isabelle 环境中子目标证明的优势，SubgoalXL 在标准 miniF2F 数据集上的 Isabelle 中达到了 56.1% 的新纪录，标志着绝对提升 4.9%。值得注意的是，SubgoalXL 成功解决了 miniF2F 中的 41 道 AMC12、9 道 AIME 和 3 道 IMO 问题。这些结果强调了最大化有限数据效用和采用针对性指导在形式化定理证明中进行复杂推理的有效性，为 AI 推理能力的持续进步做出了贡献。

7. 过程驱动的 Lean 4 自动形式化

基本信息

  • 论文地址：Process-Driven Autoformalization in Lean 4
  • 关键词：Large Language Models, Autoformalization, Lean 4, Formal Math, Process Supervision, Formal Reasoning, Mathematical Reasoning, AI for Math, Automated Theorem Proving
  • 领域：neurosymbolic & hybrid AI systems (physics-informed, logic & formal reasoning, etc.)
  • TLDR: We introduces the FormL4 benchmark to evaluate autoformalization in Lean 4, along with a process-supervised verifier that enhances the accuracy of LLMs in converting informal statements and proofs into formal ones.

内容概要：提出了 FormL4 基准，以及 Lean4 编译器反馈的过程驱动的自动形式化。

摘要

自动形式化，即将自然语言数学转换为形式语言，为推进数学推理提供了巨大的潜力。然而，现有努力仅限于具有大量在线语料库的形式语言，并且难以跟上像 Lean 4 这样快速发展的语言的步伐。为了弥合这一差距，我们提出了一个大规模数据集 Formalization$ for Lean4 (数据集)，旨在全面评估大型语言模型 (LLMs) 的自动形式化能力，涵盖自然语言和形式语言中的陈述和证明。此外，我们引入了 Process-Driven Autoformalization (方法) 框架，该框架利用 Lean 4 编译器的精确反馈来增强自动形式化。广泛的实验表明，PDA 提高了自动形式化能力，使得编译器准确性和人类评估分数在使用较少过滤训练数据的情况下更高。此外，当使用包含详细过程信息的数据进行微调时，PDA 展示了增强的数据利用率，从而在 Lean 4 的自动形式化方面取得了更显著的改进。

8. miniCTX: 带有长上下文的神经定理证明

基本信息

  • 论文地址：miniCTX: Neural Theorem Proving with (Long-)Contexts
  • 关键词：Neural theorem proving, Formal mathematics, Benchmark dataset
  • 领域：datasets and benchmarks
  • TLDR: We introduce a context-rich dataset and toolkit for evaluation of neural theorem proving under a more realistic scenario.

核心内容：提出挖掘模型上下文的能力的基准 miniCTX 和标注工具 ntp-toolkit。

摘要

现实世界中的形式化定理证明通常依赖于丰富的上下文信息，包括定义、引理、注释、文件结构等。本文介绍了 miniCTX\texttt{miniCTX}，它测试模型在证明依赖于训练中未见的新上下文的形式数学定理的能力。miniCTX\texttt{miniCTX} 包含源自真实 Lean 项目和教材的定理，每个定理都与一个可能跨越数万个标记的上下文相关联。模型的任务是在给定定理存储库中的代码访问权限的情况下证明定理，这些代码包含了证明所需的上下文。作为 miniCTX\texttt{miniCTX} 的基线，我们测试了基于前文微调和提示方法。这两种方法都显著优于仅依赖状态信息的传统方法。我们发现，这种使用上下文的能力并未被之前的基准测试（如 miniF2F\texttt{miniF2F}）所捕捉。伴随 miniCTX\texttt{miniCTX}，我们提供了 ntp-toolkit\texttt{ntp-toolkit}，用于自动提取和注释定理证明数据，使得将新项目添加到 miniCTX\texttt{miniCTX} 中变得容易，确保上下文在训练中未被见过。miniCTX\texttt{miniCTX} 为神经定理证明提供了一个具有挑战性和现实性的评估。

9. 通过奖励 LLMs 分层分解证明来进行形式定理证明

基本信息

  • 论文地址：Formal Theorem Proving by Rewarding LLMs to Decompose Proofs Hierarchically
  • 关键词：formal theorem proving, large language models, reinforcement learning
  • 领域：neurosymbolic & hybrid AI systems (physics-informed, logic & formal reasoning, etc.)
  • TLDR: We design an RL-based training algorithm that encourages LLMs to write formal proofs by proposing and proving new lemmas, mimicking how mathematicians train themselves.

核心思想：基于强化学习的算法，鼓励 LLMs 通过提出和证明新引理来编写形式证明，模仿数学家的训练方式。

摘要

数学定理证明是检验大型语言模型深度和抽象推理能力的重要测试平台。本文专注于提升大型语言模型在允许自动化证明验证/评估的形式化语言中撰写证明的能力。大多数先前的研究为定理证明器提供了人工编写的引理，这种设置被认为过于简化，未能充分测试证明器的规划和分解能力。相反，我们在一个更自然的设置中进行研究，即在测试时未向定理证明器提供直接相关的引理。我们设计了一种基于强化学习的训练算法，鼓励模型将定理分解为引理，证明这些引理，然后利用这些引理来证明定理。我们的奖励机制灵感来源于数学家的自我训练方式：即使当前模型难以证明某个定理，只要在过程中提出并证明了正确且新颖的引理，模型仍会获得奖励。在训练过程中，我们的模型证明了37.7%不在训练数据集中的引理。在测试一组保留定理时，与监督微调模型相比，我们的模型将通过率从40.8%提升至45.5%。

10. 与大型语言模型协作证明定理：使用 ProofRefiner 增强形式化证明

基本信息

核心思想：证明过程的助手，ProofRefiner 智能体

定理证明对大型语言模型（LLMs）提出了重大挑战，因为形式化证明可以通过像 Lean 这样的证明助手严格验证，容不得任何错误。现有的基于 LLM 的证明器通常独立运作，但在处理复杂和新颖的定理时往往力不从心，而这些定理恰恰需要人类洞察力。为此，我们提出了一种新框架，将 LLMs 定位为定理证明中的协作助手。该框架实现了 LLM 推理与 Lean 环境的无缝集成，允许开发者构建各种证明自动化工具。这些工具提供诸如建议证明步骤、完成中间目标、选择相关前提等功能，从而提升定理证明过程。用户可以利用我们预训练的模型，或集成自己的模型，支持本地和云端执行。实验结果表明，我们的方法在辅助人类和自动化定理证明方面比现有的基于规则的系统更有效。此外，我们引入了一个名为 ProofRefiner 的系统，通过动态对话调整来精炼问题和答案，确保相关性和精确性。

11. “Lean” 于质量：高质量数据如何在自动形式化中胜过多语言多样性数据

基本信息

核心思想：通过高质量提示和回译策略提升自动形式化性能。

摘要

自动形式化，即将非正式的数学语言转换为正式的规范和证明，对于当前最先进的大型语言模型来说仍然是一项艰巨的任务。现有研究对性能差距提出了不同的解释。一方面，大型语言模型在翻译任务上表现出色，表明它们在自动形式化方面具有巨大潜力。另一方面，标准语言模型的定量推理能力有限，导致在自动形式化和后续的形式定理证明任务上表现不佳。为此，我们引入了一种新颖的方法，利用带有手工精选提示的回译技术来增强语言模型的数学能力，特别针对标记数据稀缺的挑战。具体而言，我们评估了这一策略的三种主要变体：(1) 实时（在线）回译，(2) 蒸馏（离线）回译结合少样本放大，以及(3) 与证明状态信息集成的逐行证明分析。每种变体都旨在优化数据质量而非数量，专注于生成证明的高保真度而非数据规模。我们的研究结果表明，采用我们提出的方法生成优先考虑质量而非数量的合成数据，可以提升大型语言模型在自动形式化方面的性能，这一性能通过ProofNet等标准基准进行衡量。关键在于，我们的方法在使用极少数令牌的情况下超越了预训练模型。我们还通过战略提示和回译展示，我们的方法在ProofNet上的表现优于使用大量多语言数据集（如MMA）进行微调的模型，且仅使用了1/150的令牌。综合来看，我们的方法展示了一种有前景的新途径，显著减少了形式化证明所需的资源，从而加速了数学领域的AI发展。

12. 重新思考并改进自动形式化：迈向忠实度指标和基于依赖检索的方法

基本信息

核心内容：提出一种新的神经符号评估方法 BEq 和基于依赖检索的 RAutoformalizer，用于改进陈述的自动形式化，并构建了新的基准 Con-NF 进行评估。

摘要

作为形式验证的核心组成部分，命题陈述的自动形式化已被广泛研究，包括来自机器学习社区近期的努力，但这仍然是一个公认的困难和开放的问题。本文深入探讨了两个关键但未充分探索的差距：1）缺乏忠实且普遍的自动形式化结果评估；2）缺乏上下文信息，导致形式定义和定理的严重幻觉。为了解决第一个问题，我们提出了 BEq（双向扩展定义等价，Bidirectional Extended Definitional Equivalence），一种自动的神经符号方法，用于确定两个形式陈述之间的等价性，该方法基于形式基础并与人类直觉高度一致。对于第二个问题，我们提出了 RAutoformalizer（检索增强的自动形式化器，Retrieval-augmented Autoformalizer），通过依赖检索从形式库中检索潜在依赖对象来增强陈述的自动形式化。我们解析库的依赖关系，并提出通过依赖的拓扑顺序结构化地形式化形式对象。为了评估 OOD 泛化和研究级能力，我们构建了一个新的基准 Con-NF，包含 961 对来自前沿数学研究的非形式化-形式化陈述对。大量实验验证了我们提出方法的有效性。特别是，BEq 在 200 个多样化的形式陈述对上进行了评估，具有专家注释的等价标签，显示出显著提高的准确率（82.50% → 90.50%）和精确率（70.59% → 100.0%）。这对于依赖检索，建立了一个性能优异的基线。所提出的 RAutoformalizer 在分布内 ProofNet 基准（12.83% → 18.18%，BEq@8）和 OOD Con-NF 场景（4.58% → 16.86%，BEq@8）中均显著优于 SOTA 基线。代码、数据和模型将公开。

13. FormalAlign: 用于自动形式化的自动化对齐评估

基本信息

  • 论文地址：FormalAlign: Automated Alignment Evaluation for Autoformalization
  • 关键词：Large Language models, Autoformalization, Lean 4, Formal Math, AI for Math
  • 领域：applications to computer vision, audio, language, and other modalities
  • TLDR: FormalAlign is a framework that automatically evaluates the alignment between informal and formal mathematical proofs, significantly improving performance and reducing reliance on manual verification.

核心思想：通过自动评估非正式和形式化数学证明的对齐，提高性能并减少对手动验证的依赖。

摘要

自动形式化旨在将非正式的数学证明转换为机器可验证的格式，弥合自然语言与形式语言之间的差距。然而，确保非正式与形式化陈述之间的语义对齐仍然是一个挑战。现有方法严重依赖人工验证，阻碍了可扩展性。为此，我们引入了 FormalAlign，一个用于自动评估自动形式化中自然语言与形式语言对齐的框架。FormalAlign 在自动形式化序列生成任务和输入输出之间的表示对齐上进行训练，采用结合了相互增强的自动形式化与对齐任务的双重损失。通过在我们提出的对齐策略增强的四个基准上进行评估，FormalAlign 展示了优越的性能。在我们的实验中，FormalAlign 优于 GPT-4，在 \forml-Basic 上实现了 11.58% 的对齐选择得分提升（99.21% 对 88.91%），在 MiniF2F-Valid 上提升了 3.19%（66.39% 对 64.34%）。这种有效的对齐评估显著减少了人工验证的需求。

14. CARTS: 通过多样化策略校准和抗偏置树搜索推进神经定理证明

基本信息

核心思想：通过多样化策略校准和抗偏置树搜索，增加多样性并减少扩展冗余证明路径的搜索成本。

摘要

近年来，神经定理证明的进展将大型语言模型与蒙特卡洛树搜索（MCTS）等树搜索算法相结合，其中语言模型提出策略，树搜索找到完整的证明路径。然而，语言模型提出的许多策略在语义或战略上趋于相似，减少了多样性并增加了扩展冗余证明路径的搜索成本。随着计算规模的扩大和每个状态下探索的策略增多，这一问题加剧。此外，训练的价值函数由于数据构建的偏差，存在假阴性、标签不平衡和领域差距的问题。为应对这些挑战，我们提出了CARTS（多样化策略校准与抗偏树搜索），它在平衡策略多样性和重要性的同时校准模型信心。CARTS还引入了偏好建模和一个与有效策略比率相关的调整项，以提高价值函数的抗偏性。实验结果表明，CARTS在miniF2F-test基准上持续优于先前的方法，达到了49.6%的pass@l率。进一步分析证实，CARTS提高了策略多样性，并带来更平衡的树搜索。

15. 3D-Prover：基于行列式点过程的多样性驱动定理证明

基本信息

  • 论文地址：3D-Prover: Diversity Driven Theorem Proving With Determinantal Point Processes
  • 关键词：Theorem Proving, Formal Reasoning, Search, Representation Learning, Pruning, Filtering, Diversity
  • 领域：neurosymbolic & hybrid AI systems (physics-informed, logic & formal reasoning, etc.)
  • TLDR: Pruning proof search to diverse, high quality subsets based on their predicted outcome.

核心思想：数据增强，判断语义相似性，增强搜索多样性。

自动形式推理中的一个关键挑战是难以处理的搜索空间，该搜索空间随着证明深度指数增长，这种分支由大量可应用于给定目标的候选证明策略引起。然而，其中许多策略在语义上相似或导致执行错误，在这两种情况下都浪费了宝贵的资源。我们解决了使用从先前证明尝试生成的合成数据来有效修剪此搜索的问题。首先，我们证明可以生成能够捕获对证明环境的影响、成功的可能性和执行时间的语义感知策略表示。然后，我们提出了一种新的过滤机制，利用这些表示来选择语义多样和高质量的策略，使用行列式点过程。我们的方法 3D-Prover 被设计为通用的，可以增强任何基础策略生成器。我们通过增强 ReProver LLM，在 miniF2F-valid 和 miniF2F-test 基准上证明了 3D-Prover 的有效性。我们的结果显示，这种方法提高了整体证明率，以及策略成功率、执行时间和多样性的显著改善。

16. Lean 定理的合成生成

基本信息

  • 论文地址：Synthetic Theorem Generation in Lean
  • 关键词：theorem proving, large language model, synthetic data generation, Lean
  • 领域：neurosymbolic & hybrid AI systems (physics-informed, logic & formal reasoning, etc.)
  • TLDR: A new synthetic theorem generator for Lean creates diverse, correct-by-construction theorems and proofs, improving training data for language models in automated theorem proving.

核心思想：通过合成定理生成器生成多样且正确的新 Lean 定理和证明。

摘要

将大型语言模型（LLMs）应用于定理证明，为推进形式化数学提供了有前景的途径。交互式定理证明器，如 Lean，提供了一个严格的框架，在这些框架内，这些模型可以协助或自动化证明发现，将其推理能力建立在可靠、可验证的形式系统之上。然而，LLMs 在该领域的潜力受到用于训练的形式化证明语料库有限可用性的限制。为解决这一限制，我们引入了一种合成定理生成器，能够生成新的 Lean 定理及其相应的证明。我们的方法采用前向推理，从现有 Lean 库中提取前提来合成新的命题。我们通过一种优化输出多样性的搜索策略探索候选推理步骤，以线性方式应用这些步骤以避免无关的证明步骤，并通过元编程执行相应的 Lean 策略来评估其效果。这些方法能够在各种数学领域中生成任意数量的新定理和证明，使用常见的 Lean 证明策略，同时通过构造确保生成定理的正确性。我们通过在合成定理上微调模型并在 miniF2F-test 基准上评估它们，展示了生成定理和训练数据的有效性。结果显示定理证明能力的提升，Falcon2-11B 模型仅在 Mathlib 上训练的准确率从 37.3% 提升至 38.5%，而在混合丰富数据集上训练的同一模型的准确率从 38.1% 提升至 39.3%。这些改进突显了我们的多样化合成数据在增强有限现有形式化证明语料库中的价值，提供了补充信息，即使与其他数据集结合，也能提升 LLMs 在定理证明任务上的性能。

17. 利用证明助手反馈增强强化学习和蒙特卡洛树搜索

基本信息

核心思想：以 Lean 验证结果作为奖励信号，通过在线强化学习改进蒙特卡洛树搜索。

摘要

Lean 是一个先进的证明助手，旨在通过提供多种交互式反馈来促进形式化定理证明。本文探讨了如何利用证明助手反馈来增强大型语言模型在构建形式化证明方面的能力。首先，我们采用在线强化学习，使用 Lean 验证结果作为奖励信号，以改进证明完成策略。这种直接的方法在提升模型与形式化验证系统的对齐方面显示出巨大潜力。此外，我们提出了 RMaxTS，这是一种蒙特卡洛树搜索的变体，采用基于内在奖励的探索策略来生成多样化的证明路径。树结构被组织起来以表示从中间策略状态的转换，这些状态是从 Lean 策略模式下给出的编译消息中提取的。内在奖励的构建旨在激励发现新的策略状态，这有助于缓解证明搜索中固有的稀疏奖励问题。这些技术带来了一种更高效的形式化证明生成规划方案，在 miniF2F 和 ProofNet 基准测试中均取得了新的最佳结果。

18. 炼金术（Alchemy）：通过符号突变增强定理证明能力

基本信息

  • 论文地址：Alchemy: Amplifying Theorem-Proving Capability Through Symbolic Mutation
  • 关键词：Synthetic Data, Neural Theorem Proving, Formal Reasoning, Lean Theorem Prover
  • 领域：applications to computer vision, audio, language, and other modalities
  • TLDR: This work proposes Alchemy, a general framework for data synthesis that constructs formal theorems through symbolic mutations.

核心思想：通过符号突变合成形式化定理数据，增强神经定理证明能力。

摘要

即使是经验丰富的专家，编写形式化证明也是一项挑战。近年来，神经定理证明（NTP）的进展显示出加速这一过程的潜力。然而，与通用文本相比，互联网上可用的形式化语料库有限，这对NTP构成了显著的数据稀缺挑战。为解决这一问题，本文提出了炼金术（Alchemy），这是一个通过符号突变构建形式化定理的数据合成通用框架。具体而言，对于Mathlib中的每个候选定理，我们识别出所有可调用的定理，这些定理可以用于重写(rewrite)或应用(apply)。随后，我们通过将陈述中的相应术语替换为其等价形式或前件来突变候选定理。结果，我们的方法将Mathlib中的定理数量增加了一个数量级，从11万增加到600万。此外，我们对这一增强语料库进行了大型语言模型的持续预训练和监督微调。实验结果表明，我们的方法在Leandojo基准测试上实现了5%的绝对性能提升。此外，我们的合成数据在分布外的miniF2F基准测试上实现了2.5%的绝对性能增益。为了提供更深入的见解，我们对合成数据的组成和训练范式进行了全面分析，为开发强大的定理证明器提供了宝贵的指导。

19. ZIP-FIT：基于压缩对齐的无嵌入数据选择方法

基本信息

核心思想：如题，基于压缩对齐的无嵌入数据选择框架，用于选择高质量、对齐的微调数据。

摘要

选择高质量、对齐的微调数据对于提升语言模型（LMs）的下游性能至关重要。在这些场景中，自动数据选择具有挑战性且通常效率低下，因为以往的方法依赖于神经嵌入或有限的 n-gram 表示来识别对齐的数据集。此外，传统的数据选择方法通常专注于增加训练数据的规模，这使得它们在计算上昂贵且数据效率低下。在这项工作中，我们介绍了 ZIP-FIT，一种无嵌入、数据高效的选择框架，利用 gzip 压缩来衡量训练数据与目标领域之间的对齐程度。我们展示了 ZIP-FIT 在为 ProofNet（一个形式化数学数据集）和 HumanEval（一个代码生成任务的基准）选择高质量数据方面，显著优于两个领先的基线方法，DSIR 和 D4。具体而言，ZIP-FIT 在计算速度上具有优势，数据选择速度比 DSIR 快 65.8%，并且达到最低交叉熵损失的速率快 85.1%。我们的发现表明，ZIP-FIT 为数据选择提供了一种可扩展和适应性强的方法，使代码生成领域的微调更加精确。通过证明无嵌入数据选择可以优于 DSIR 和 D4 等成熟方法，我们的研究为优化模型训练开辟了新途径，从而提高了机器学习工作流程的有效性和效率。

20. 通过整合大型语言模型和符号推理来证明奥数不等式

基本信息

核心思想：融合 LLMs 的数学直觉和符号推理，高效证明奥数不等式。

摘要

大型语言模型（LLMs）可以通过在证明系统中生成证明步骤（即策略）来正式证明数学定理。然而，可能的策略空间庞大且复杂，而用于形式化证明的训练数据有限，这对基于 LLMs 的策略生成构成了重大挑战。为解决这一问题，我们引入了一种神经符号策略生成器，它将 LLMs 学习的数学直觉与符号方法编码的领域特定见解相结合。这种整合的关键在于识别哪些数学推理部分最适合 LLMs，哪些适合符号方法。尽管神经符号整合的高层次思想广泛适用于各种数学问题，但本文特别关注奥数不等式（见图~\ref{fig:example}）。我们分析了人类如何解决这些问题，并将技术提炼为两种类型的策略：（1）缩放，由符号方法处理；（2）重写，由 LLMs 处理。此外，我们将符号工具与LLMs结合，以修剪和排序证明目标，实现高效的证明搜索。我们在来自多个数学竞赛的161个挑战性不等式上评估了我们的框架，取得了最先进的性能，并显著优于现有的LLMs和符号方法，而无需额外的训练数据。

20241017095537

数学竞赛

Putnam-AXIOM：用于衡量 LLMs 高级数学推理能力的功能性静态基准

基本信息

核心内容：提出 Putnam-AXIOM 基准，通过原始和变体问题评估 LLMs 的数学推理能力，揭示数据污染的影响。

提出Putnam-AXIOM基准，评估大型语言模型的高级数学推理能力，揭示数据污染对模型性能的影响。

摘要

随着大型语言模型（LLMs）的不断进步，许多用于评估其推理能力的现有基准正在变得饱和。因此，我们提出了 Putnam-AXIOM 原基准，包括来自 William Lowell Putnam 数学竞赛的 236 个数学问题及其详细的逐步解决方案。为了保持 Putnam-AXIOM 基准的有效性并减轻潜在的数据污染，我们创建了 Putnam-AXIOM 变体基准，包含 52 个问题的功能变体。通过程序化地改变问题元素，如变量和常数，我们可以生成无数新颖且同样具有挑战性的问题，这些问题在网上找不到。我们发现几乎所有模型在变体问题上的准确性都显著低于原始问题。我们的结果显示，表现最佳的模型 OpenAI 的 o1-preview 在 Putnam-AXIOM 原始基准上的准确率仅为 41.95%，而在变体数据集上的准确率相比相应的原始问题下降了约 30%。此外，我们探索了超越框选准确率的指标，以评估模型在自然语言定理证明等复杂任务上的表现，这对于深入评估推理能力至关重要，开启了推理链开放式评估的可能性。

Omni-MATH: 一个用于评估大型语言模型奥林匹克数学水平的通用基准

基本信息

核心内容：专注于数学，并包含大量经过严格人工注释的 4428 个竞赛级别问题。

摘要

大型语言模型 (LLMs) 的最新进展在数学推理能力方面取得了显著突破。然而，现有的基准如 GSM8K 或 MATH 现在已被高精度解决（例如，OpenAI o1 在 MATH 数据集上达到 94.8%），表明它们不足以真正挑战这些模型。为了填补这一空白，我们提出了一项全面且具有挑战性的基准，专门设计用于评估 LLMs 在奥林匹克级别的数学推理能力。与现有的奥林匹克相关基准不同，我们的数据集专注于数学，并包含大量经过严格人工注释的 4428 个竞赛级别问题。这些问题被精心分类为超过 33 个子领域，并跨越 10 多个不同的难度级别，从而能够全面评估模型在奥林匹克数学推理中的表现。此外，我们基于此基准进行了深入分析。我们的实验结果显示，即使是最高级的模型，OpenAI o1-mini 和 OpenAI o1-preview，在高度挑战的奥林匹克级别问题上仍面临困难，准确率分别为 60.54% 和 52.55%，突显了奥林匹克级别数学推理中的显著挑战。

SBSC: 逐步编码法提升数学奥林匹克竞赛表现

基本信息

核心思想：多轮数学推理框架 SBSC，逐步生成和执行程序解决奥林匹克级别数学问题，提升解题效率和准确性。

摘要

本文提出了一种名为逐步编码法（SBSC）的多轮数学推理框架，该框架使大型语言模型（LLMs）能够生成一系列程序来解决奥林匹克级别的数学问题。在每一轮或步骤之后，模型利用前几步的代码执行输出和程序，生成下一个子任务及其对应的程序以完成该任务。通过这种方式，SBSC 逐步导航以达到最终答案。与现有方法相比，SBSC 允许更细粒度、灵活和精确的问题解决方法。广泛的实验证明了 SBSC 在解决竞赛和奥林匹克级别数学问题上的有效性。对于 Claude-3.5-Sonnet，我们观察到 SBSC（贪婪解码）在 AMC12 上超越了现有的最先进（SOTA）程序生成推理策略，绝对提升 10.7%，在 AIME 上提升 8%，在 MathOdyssey 上提升 12.6%。鉴于 SBSC 本质上是多轮的，我们还将其贪婪解码结果与现有 SOTA 数学推理策略的自一致性解码结果进行了基准测试，并观察到在 AMC 上性能提升 6.2%，在 AIME 上提升 6.7%，在 MathOdyssey 上提升 7.4%。

GeoILP: 用于指导大规模规则归纳的合成数据集

基本信息

核心内容：GeoILP 数据集，难度高的几何数据集。

提出GeoILP数据集，用于推动大规模归纳逻辑编程任务的研究，解决现有方法在复杂语言偏见上的不足，并促进神经感知与符号规则归纳的联合学习。

摘要

归纳逻辑编程（Inductive Logic Programming, ILP）是一种旨在从数据中学习解释性规则的机器学习方法。尽管现有的ILP系统能够成功解决小规模任务，但涉及多种语言偏见的大规模应用却鲜少被探索。此外，对于大多数当前ILP系统而言，需要专家定义的语言偏见是至关重要的，这阻碍了ILP向更广泛应用的 发展。在本文中，我们介绍了 GeoILP，一个包含多种ILP任务的大规模合成数据集，涉及语言偏见的多个方面。这些 ILP 任务基于几何问题构建，难度从教科书习题到地区国际数学奥林匹克（IMO）不等，并借助推理引擎完成。这些问题经过精心选择，涵盖了所有具有挑战性的语言偏见，例如递归、谓词发明和高阶性。实验结果表明，现有的方法都无法解决GeoILP任务。此外，除了经典的符号形式数据，我们还提供了图像形式数据，以促进神经感知与符号规则归纳的联合学习发展。

AoPS 数据集：利用在线奥林匹克级数学问题进行 LLM 训练和抗污染评估

基本信息

核心内容：利用 AoPS 论坛资源自动生成高质量数学问题数据集，并构建抗污染的动态评估基准。

摘要

大型语言模型（LLMs）的进步引发了人们对其解决奥数级别数学问题能力的兴趣。然而，这些模型的训练和评估受限于现有数据集的规模和质量，因为创建如此高级问题的规模化数据需要人类专家的大量努力。此外，当前的基准测试容易受到污染，导致评估结果不可靠。本文介绍了一个自动化流程，利用“解题艺术”（AoPS）论坛的丰富资源，该论坛主要包含奥数级别问题和社区驱动的解决方案。使用开源LLMs，我们开发了一种从论坛中提取问答对的方法，生成了AoPS-Instruct数据集，包含超过65万个高质量的问答对。我们的实验表明，在 AoPS-Instruct 上微调 LLMs 可以提升其在各个基准测试中的推理能力。此外，我们构建了一个自动化流程，引入了LiveAoPSBench，这是一个基于最新论坛数据且带有时间戳的动态评估集，提供了一个抗污染的基准来评估LLM性能。值得注意的是，我们观察到LLM性能随时间显著下降，这表明其在旧例题上的成功可能源于预训练的暴露而非真正的推理能力。我们的工作展示了一种可扩展的方法，用于创建和维护大规模、高质量的先进数学推理数据集，为LLMs在此领域的能力和局限性提供了宝贵见解。我们的基准测试可在livemathbench.github.io/leaderboard获取。

注：目前该链接无效，这个工作很有价值，但双盲阶段应该用匿名链接提交吧？

数据集

MathOdyssey: 使用 OdysseyMath 数据集评估大型语言模型在数学问题解决能力上的基准测试

基本信息

核心内容：新开发的“Math Odyssey”数据集，包含高中和大学水平的多样的数学问题。

摘要

大型语言模型（LLMs）在自然语言理解和问题解决能力上取得了显著进展。尽管如此，大多数LLMs在解决数学问题方面仍面临挑战，主要原因是数学问题需要复杂的推理能力。本文通过新开发的“Math Odyssey”数据集，探讨了LLMs的数学问题解决能力。该数据集包含高中和大学水平的多样的数学问题，由知名机构的专家创建，旨在严格测试LLMs在高级问题解决场景中的表现，并覆盖更广泛的学科领域。通过向AI社区提供Math Odyssey数据集，我们旨在促进对AI在复杂数学问题解决能力上的理解和改进。我们对开源模型（如Llama-3）和闭源模型（如GPT系列和Gemini模型）进行了基准测试。结果显示，尽管LLMs在常规和中等难度任务上表现良好，但在奥赛级别问题和复杂的大学水平问题上仍面临显著挑战。我们的分析表明，开源模型和闭源模型之间的性能差距正在缩小，但在最棘手的问题上仍存在重大挑战。这项研究强调了继续研究以提升LLMs数学推理能力的必要性。数据集、结果和评估代码已公开可用。

29. U-MATH: A University-Level Benchmark for Evaluating Mathematical Skills in LLMs

基本信息

  • 论文地址：U-MATH: A University-Level Benchmark for Evaluating Mathematical Skills in LLMs
  • 关键词：Large Language Models (LLMs), Mathematical Reasoning, Benchmarking, University-Level Mathematics, Multimodal, Automatic Evaluation, Solution Assessment
  • 领域：datasets and benchmarks
  • TLDR: U-MATH, a challenging university-level math benchmark with both textual and visual problems, and additional μ-MATH benchmark to evaluate solution assessment capabilities.

标题

U-MATH: 评估 LLMs 数学技能的大学级别基准

U-MATH: 用于评估大型语言模型中大学水平数学技能的基准

核心思想

引入 U-MATH 和 μ-MATH 基准，评估 LLMs 在大学级别数学问题和解决方案评估中的表现。

提出U-MATH基准数据集，用于全面评估大型语言模型在大学水平数学问题上的表现，并引入μ\mu-MATH评估模型答案评判能力。

摘要

The current evaluation of mathematical skills in LLMs is limited, as existing benchmarks are relatively small, primarily focus on elementary and high-school problems, or lack diversity in topics. Additionally, the inclusion of visual elements in tasks remains largely under-explored.

To address these gaps, we introduce U-MATH, a novel benchmark of 1,125 unpublished open-ended university-level problems sourced from teaching materials. It is balanced across six core subjects, with 20% of problems requiring image understanding. Given the open-ended nature of U-MATH problems, we employ an LLM to judge the correctness of generated solutions. To this end, we release μ\boldsymbol\mu-MATH, an additional dataset to evaluate the LLMs’ capabilities in assessing solutions.

The evaluation of general domain, math-specific, and multimodal LLMs highlights the challenges presented by U-MATH. Our findings reveal that LLMs achieve a maximum accuracy of only 53% on text-based tasks, with even lower 30% on visual problems. The solution assessment proves challenging for LLMs, with the best LLM judge having an F1-score of 76% on μ\mu-MATH.

We open-source U-MATH, μ\mu-MATH, and evaluation code on GitHub.

当前对 LLMs 数学技能的评估存在局限性，因为现有基准相对较小，主要集中在小学和中学问题，或者在主题多样性方面不足。此外，任务中视觉元素的包含仍未得到充分探索。为了解决这些差距，我们引入了 U-MATH，这是一个包含 1,125 个未发表的开放式大学级别问题的全新基准，源自教学材料。它在六个核心科目之间保持平衡，其中 20% 的问题需要图像理解。鉴于 U-MATH 问题的开放性，我们采用 LLM 来判断生成解决方案的正确性。为此，我们发布了 μ-MATH，一个额外的数据集，用于评估 LLMs 在评估解决方案方面的能力。对通用领域、数学特定和多模态 LLMs 的评估突显了 U-MATH 带来的挑战。我们的研究结果表明，LLMs 在基于文本的任务上最高准确率仅为 53%，而在视觉问题上甚至更低，仅为 30%。解决方案评估对 LLMs 来说也具有挑战性，最佳 LLM 评判在 μ-MATH 上的 F1 分数为 76%。我们在 GitHub 上开源了 U-MATH、μ-MATH 和评估代码。

当前对大型语言模型（LLMs）中数学技能的评估存在局限性，因为现有的基准数据集相对较小，主要集中于小学和中学问题，或者缺乏主题多样性。此外，任务中视觉元素的纳入也尚未得到充分探索。为填补这些空白，我们引入了U-MATH，这是一个包含1,125个未发表、开放式大学水平问题的全新基准数据集，这些题目来源于教学材料。该数据集在六个核心学科中保持平衡，其中20%的问题需要图像理解能力。鉴于U-MATH问题的开放式特性，我们使用一个LLM来判断生成答案的正确性。为此，我们发布了**μ\boldsymbol\mu-MATH**，一个额外的数据集，用于评估LLMs评估答案的能力。通过对通用领域、数学特定领域和多模态LLMs的评估，U-MATH所呈现的挑战得以凸显。我们的研究发现，LLMs在基于文本的任务上最高准确率仅为53%，而在视觉问题上更是低至30%。解决方案评估对LLMs而言同样具有挑战性，表现最佳的LLM评判者在μ\mu-MATH上的F1分数为76%。我们在GitHub上开源了U-MATH、μ\mu-MATH及评估代码。

47. UGMathBench: A Diverse and Dynamic Benchmark for Undergraduate-Level Mathematical Reasoning with Large Language Models

基本信息

标题

UGMathBench: 一个针对本科生数学推理的大语言模型多样化动态基准

UGMathBench: 一个多样化和动态的基准，用于评估大型语言模型在本科水平数学推理上的能力

核心思想

引入 UGMathBench 基准，评估大语言模型在本科数学推理中的表现，并提出有效准确率和推理差距两个关键指标。

引入UGMathBench基准，评估大型语言模型在本科水平数学推理上的能力，并提出有效准确率和推理差距两个关键指标。

摘要

Large Language Models (LLMs) have made significant strides in mathematical reasoning, underscoring the need for a comprehensive and fair evaluation of their capabilities. However, existing benchmarks often fall short, either lacking extensive coverage of undergraduate-level mathematical problems or probably suffering from test-set contamination. To address these issues, we introduce UGMathBench, a diverse and dynamic benchmark specifically designed for evaluating undergraduate-level mathematical reasoning with LLMs. UGMathBench comprises 5,062 problems across 16 subjects and 111 topics, featuring 10 distinct answer types. Each problem includes three randomized versions, with additional versions planned for release as the leading open-source LLMs become saturated in UGMathBench. Furthermore, we propose two key metrics: effective accuracy (EAcc), which measures the percentage of correctly solved problems across all three versions, and reasoning gap (Δ\Delta), which assesses reasoning robustness by calculating the difference between the average accuracy across all versions and EAcc. Our extensive evaluation of 23 leading LLMs reveals that the highest EAcc achieved is 56.3% by OpenAI-o1-mini, with large Δ\Delta values observed across different models. This highlights the need for future research aimed at developing “large reasoning models” with high EAcc and Δ=0\Delta = 0. We anticipate that the release of UGMathBench, along with its detailed evaluation codes, will serve as a valuable resource to advance the development of LLMs in solving mathematical problems.

大语言模型 (LLMs) 在数学推理方面取得了显著进展，突显了对其能力进行全面和公平评估的必要性。然而，现有基准往往存在不足，要么缺乏对本科生数学问题的广泛覆盖，要么可能受到测试集污染的影响。为了解决这些问题，我们引入了 UGMathBench，这是一个专门为评估 LLMs 在本科生数学推理能力而设计的多样化动态基准。UGMathBench 包含 5,062 个问题，涵盖 16 个学科和 111 个主题，具有 10 种不同的答案类型。每个问题包括三个随机版本，并计划随着领先的开源 LLMs 在 UGMathBench 中达到饱和时发布更多版本。此外，我们提出了两个关键指标：有效准确率 (EAcc)，用于衡量所有三个版本中正确解决问题的百分比；推理差距 (Δ\Delta)，通过计算所有版本的平均准确率与 EAcc 之间的差异来评估推理的稳健性。我们对 23 个领先的 LLMs 进行了广泛评估，发现 OpenAI-o1-mini 达到了 56.3% 的最高 EAcc，不同模型之间观察到较大的 Δ\Delta 值。这突显了未来研究需要开发具有高 EAcc 和 Δ=0\Delta = 0 的“大推理模型”。我们预计，UGMathBench 的发布及其详细的评估代码将成为推动 LLMs 解决数学问题发展的重要资源。

大型语言模型（LLMs）在数学推理方面取得了显著进展，突显了对它们能力进行全面和公平评估的需求。然而，现有的基准测试往往存在不足，要么缺乏对本科水平数学问题的广泛覆盖，要么可能受到测试集污染的影响。为解决这些问题，我们引入了UGMathBench，一个专门为评估大型语言模型在本科水平数学推理能力而设计的多样化和动态基准。UGMathBench包含5,062个问题，涵盖16个学科和111个主题，具有10种不同的答案类型。每个问题包括三个随机化版本，随着领先的开源LLMs在UGMathBench中趋于饱和，计划发布更多版本。此外，我们提出了两个关键指标：有效准确率（EAcc），衡量所有三个版本中正确解决问题百分比；推理差距（Δ\Delta），通过计算所有版本的平均准确率与EAcc之间的差异，评估推理的稳健性。我们对23个领先LLMs的广泛评估显示，OpenAI-o1-mini达到了最高的EAcc为56.3%，不同模型中观察到较大的Δ\Delta值。这突显了未来研究需要开发具有高EAcc和Δ=0\Delta = 0的“大型推理模型”。我们预计，UGMathBench的发布及其详细的评估代码，将成为推进LLMs解决数学问题发展的宝贵资源。

28. Can External Validation Tools Improve Annotation Quality for LLM-as-a-Judge?

基本信息

标题

外部验证工具能否提高 LLM 作为评判者的标注质量？

外部验证工具能否提高大语言模型作为评判者的标注质量？

核心思想

通过外部验证工具增强 AI 标注系统，以提高在长篇事实、数学和代码任务中的反馈质量。

利用外部验证工具提高AI标注者在特定领域（长篇事实、数学和代码任务）的反馈质量。

摘要

Pairwise preferences over model responses are widely collected to evaluate and provide feedback to large language models (LLMs). Given two alternative model responses to the same input, a human or AI annotator selects the “better” response. This approach can provide feedback for domains where other hard-coded metrics are difficult to obtain (e.g., quality of a chat interactions), thereby helping measure model progress or model fine-tuning (e.g., via reinforcement learning from human feedback, RLHF). However, for some domains it can be tricky to obtain such pairwise comparisons in high quality - from AI and humans. For example, for responses with many factual statements or complex code, annotators may overly focus on simpler features such as writing quality rather the underlying facts or technical details. In this work, we explore augmenting standard AI annotator systems with additional tools to improve performance on three challenging response domains: long-form factual, math and code tasks. We propose a tool-using agentic system to provide higher quality feedback on these domains. Our system uses web-search and code execution to ground itself based on external validation, independent of the LLM’s internal knowledge and biases. We provide extensive experimental results evaluating our method across the three targeted response domains as well as general annotation tasks, using RewardBench data (incl. AlpacaEval and LLMBar), as well as three new datasets for areas where pre-existing datasets are saturated. Our results indicate that external tools can indeed improve AI annotator performance in many, but not all, cases. More generally, our experiments highlight the high variability of AI annotator performance with respect to simple parameters (e.g., prompt) and the need for improved (non-saturated) annotator benchmarks. We share our data and code publicly.

在评估和向大型语言模型（LLM）提供反馈时，广泛收集模型响应的成对偏好。对于同一输入的两个替代模型响应，人类或 AI 标注者会选择“更好”的响应。这种方法可以在难以获得其他硬编码指标的领域（例如，聊天交互的质量）提供反馈，从而帮助衡量模型进展或模型微调（例如，通过人类反馈的强化学习，RLHF）。然而，对于某些领域，获取高质量的成对比较可能很棘手——无论是来自 AI 还是人类。例如，对于包含许多事实陈述或复杂代码的响应，标注者可能会过度关注写作质量等简单特征，而不是基础事实或技术细节。在这项工作中，我们探讨了通过增加额外工具来增强标准 AI 标注系统，以提高在三个具有挑战性的响应领域（长篇事实、数学和代码任务）中的表现。我们提出了一种使用工具的代理系统，以在这些领域提供更高质量的反馈。我们的系统使用网络搜索和代码执行来基于外部验证进行自我定位，独立于 LLM 的内部知识和偏见。我们提供了广泛的实验结果，评估了我们的方法在三个目标响应领域以及一般标注任务中的表现，使用了 RewardBench 数据（包括 AlpacaEval 和 LLMBar），以及针对现有数据集饱和的三个新数据集。我们的结果表明，外部工具确实可以在许多情况下提高 AI 标注者的表现，但并非所有情况。更广泛地说，我们的实验突显了 AI 标注者性能相对于简单参数（例如，提示）的高度可变性，以及改进（非饱和）标注基准的必要性。我们公开分享了我们的数据和代码。

为了评估和反馈大型语言模型（LLMs），广泛收集了模型响应的成对偏好。给定同一输入的两个备选模型响应，由人类或AI标注者选择“更好”的响应。这种方法可以为难以获得其他硬编码指标的领域（例如，聊天交互的质量）提供反馈，从而帮助衡量模型进展或模型微调（例如，通过人类反馈的强化学习，RLHF）。然而，在某些领域，从AI和人类那里获得高质量的成对比较可能较为棘手。例如，对于包含许多事实陈述或复杂代码的响应，标注者可能过度关注写作质量，而忽略了底层事实或技术细节。在这项工作中，我们探讨了通过增加额外工具来增强标准AI标注系统，以提高在三个具有挑战性的响应领域（长篇事实、数学和代码任务）的性能。我们提出了一种使用工具的代理系统，以在这些领域提供更高质量的反馈。我们的系统利用网络搜索和代码执行来基于外部验证进行自我校准，独立于LLM的内部知识和偏见。我们提供了广泛的实验结果，评估了我们的方法在三个目标响应领域以及一般标注任务中的表现，使用了RewardBench数据（包括AlpacaEval和LLMBar），以及三个针对现有数据集饱和领域的新数据集。结果表明，外部工具确实可以在许多（但并非所有）情况下提高AI标注者的性能。更广泛地说，我们的实验突显了AI标注者性能对简单参数（例如，提示）的高度变异性，以及改进（非饱和）标注者基准的必要性。我们公开分享了我们的数据和代码。

32. EXecution-Eval: Can language models execute real-world code?

基本信息

标题

EXecution-Eval: 语言模型能否执行真实世界的代码？

EXecution-Eval: 语言模型能否执行真实代码？

核心思想

引入 EXecution-Eval 基准测试，评估语言模型执行代码和预测程序状态的能力，解决现有评估的限制，并揭示模型在复杂任务中的挑战。

提出EXecution-Eval基准测试，评估语言模型执行真实代码和预测程序状态的能力，揭示其在复杂任务中的局限性。

摘要

As language models (LLMs) advance, traditional benchmarks face challenges of dataset saturation and disconnection from real-world performance, limiting our understanding of true model capabilities. We introduce EXecution-Eval (EXE), a benchmark designed to assess LLMs’ ability to execute code and predict program states. EXE attempts to address key limitations in existing evaluations: difficulty scaling, task diversity, training data contamination, and cost-effective scalability.
Comprising over 30,000 tasks derived from 1,000 popular Python repositories on GitHub, EXE spans a range of context lengths and algorithmic complexities. Tasks require models to execute code, necessitating various operations including mathematical reasoning, logical inference, bit manipulation, string operations, loop execution, and maintaining multiple internal variable states during computation. Our methodology involves: (a) selecting and preprocessing GitHub repositories, (b) generating diverse inputs for functions, © executing code to obtain ground truth outputs, and (d) formulating tasks that require models to reason about code execution. This approach allows for continuous new task generation for as few as 1,200 tokens, significantly reducing the risk of models “training on the test set.”
We evaluate several state-of-the-art LLMs on EXE, revealing insights into their code comprehension and execution capabilities. Our results show that even the best-performing models struggle with complex, multi-step execution tasks, highlighting specific computational concepts that pose the greatest challenges for today’s LLMs. Furthermore, we review EXE’s potential for finding and predicting errors to aid in assessing a model’s cybersecurity capabilities. We propose EXE as a sustainable and challenging testbed for evaluating frontier models, offering potential insights into their internal mechanistic advancement

随着语言模型（LLMs）的进步，传统的基准测试面临着数据集饱和和与实际性能脱节的问题，限制了我们对模型真实能力的理解。我们引入了 EXecution-Eval（EXE），这是一个旨在评估 LLMs 执行代码和预测程序状态能力的基准测试。EXE 试图解决现有评估中的关键限制：难以扩展、任务多样性、训练数据污染和成本效益扩展。EXE 包含从 GitHub 上 1,000 个流行的 Python 仓库中提取的超过 30,000 个任务，涵盖了广泛的内容长度和算法复杂性。任务要求模型执行代码，需要各种操作，包括数学推理、逻辑推理、位操作、字符串操作、循环执行以及在计算过程中维护多个内部变量状态。我们的方法包括：（a）选择和预处理 GitHub 仓库，（b）为函数生成多样化的输入，（c）执行代码以获得基准输出，（d）制定需要模型推理代码执行的任务。这种方法允许以最少 1,200 个标记持续生成新任务，显著降低了模型“在测试集上训练”的风险。我们在 EXE 上评估了几种最先进的 LLMs，揭示了它们在代码理解和执行能力方面的见解。我们的结果显示，即使是最优秀的模型在复杂的多步骤执行任务中也面临困难，突出了对当今 LLMs 构成最大挑战的特定计算概念。此外，我们探讨了 EXE 在发现和预测错误方面的潜力，以帮助评估模型的网络安全能力。我们提议将 EXE 作为一个可持续且具有挑战性的测试平台，用于评估前沿模型，提供对其内部机制进展的潜在见解。

随着语言模型（LLMs）的进步，传统基准测试面临数据集饱和和与真实世界性能脱节的问题，限制了我们对模型真实能力的理解。本文介绍了EXecution-Eval（EXE），一个旨在评估LLMs执行代码和预测程序状态能力的基准测试。EXE试图解决现有评估中的关键局限性：难以扩展、任务多样性不足、训练数据污染以及成本效益的可扩展性。EXE包含超过30,000个任务，这些任务源自GitHub上1,000个热门Python仓库，涵盖了不同长度的上下文和算法复杂度。任务要求模型执行代码，涉及数学推理、逻辑推断、位操作、字符串操作、循环执行以及在计算过程中维护多个内部变量状态等操作。我们的方法包括：（a）选择和预处理GitHub仓库，（b）为函数生成多样化输入，（c）执行代码以获取真实输出，（d）制定需要模型推理代码执行的任务。这种方法允许以低至1,200个标记连续生成新任务，显著降低了模型“在测试集上训练”的风险。我们在EXE上评估了多个最先进的LLMs，揭示了它们在代码理解和执行能力方面的见解。结果显示，即使是表现最佳的模型在复杂的多步骤执行任务中也面临困难，突出了对当今LLMs最具挑战性的特定计算概念。此外，我们还探讨了EXE在发现和预测错误方面的潜力，以帮助评估模型的网络安全能力。我们提出EXE作为一个可持续且具有挑战性的测试平台，用于评估前沿模型，提供对其内部机制进步的潜在洞察。

58. Improving AI via Novel Computational Models and Programming Challenges

基本信息

标题

通过新颖的计算模型和编程挑战提升人工智能

通过新型计算模型和编程挑战提升人工智能

核心思想

通过引入新颖的计算模型和编程挑战来提升人工智能的适应性和问题解决能力。

通过引入新型计算模型和编程挑战，测试和提升人工智能的适应性与问题解决能力

摘要

AI, like humans, should be able to adapt and apply learned knowledge across diverse domains, such as computational models, mathematical/formal systems, and programming languages to solve problems. Current AI training often relies on existing systems, which limits its ability to generate original solutions or generalize across unfamiliar contexts. To address this, we propose a new computational model along with a revised programming language tailored to this model. By challenging AI to write, analyze, or verify programs within these new frameworks, and by utilizing a virtual machine for evaluation, we aim to test and enhance the AI’s adaptability and problem-solving capabilities in a verifiable manner.

人工智能，如同人类一样，应当能够在不同的领域中适应并应用所学知识，例如计算模型、数学/形式系统以及编程语言来解决问题。当前的人工智能训练通常依赖于现有系统，这限制了其生成原创解决方案或在不熟悉的环境中进行泛化的能力。为了解决这一问题，我们提出了一种新的计算模型，并设计了一种适应此模型的修订编程语言。通过挑战人工智能在这些新框架内编写、分析或验证程序，并利用虚拟机进行评估，我们旨在以可验证的方式测试并增强人工智能的适应性和问题解决能力。

人工智能应像人类一样，能够适应并将在不同领域学到的知识应用于解决各类问题，例如计算模型、数学/形式系统以及编程语言。当前的人工智能训练往往依赖于现有系统，这限制了其生成原创解决方案或在陌生环境中进行泛化的能力。为解决这一问题，本文提出了一种新型计算模型以及针对该模型优化的编程语言。通过挑战人工智能在这些新框架内编写、分析或验证程序，并利用虚拟机进行评估，我们旨在以可验证的方式测试并提升人工智能的适应性和问题解决能力。

34. Exposing the Achilles’ Heel: Evaluating LLMs Ability to Handle Mistakes in Mathematical Reasoning

基本信息

标题

揭露阿喀琉斯之踵：评估大型语言模型处理数学推理中错误的能力

揭示阿喀琉斯之踵：评估大型语言模型处理数学推理错误的能力

核心思想

评估LLMs在数学应用题中检测和纠正推理错误的能力，提出MWP-MISTAKE数据集并进行模型基准测试。

通过MWP-MISTAKE数据集评估LLMs在数学应用题中检测和纠正推理错误的能力，揭示其优势和局限性。

摘要

Large Language Models (LLMs) have significantly impacted the field of Math Word Problems (MWPs), transforming how these problems are approached and solved, particularly in educational contexts. However, existing evaluations often focus on final accuracy, neglecting the critical aspect of reasoning capabilities. This work addresses that gap by evaluating LLMs’ abilities to detect and correct reasoning mistakes. We present a novel dataset, MWP-MISTAKE, containing MWPs with both correct and incorrect reasoning steps generated through rule-based methods and smaller language models. Our comprehensive benchmarking of state-of-the-art models such as GPT-4o and GPT4 uncovers important insights into their strengths and limitations. While GPT-4o excels in mistake detection and rectification, gaps remain, particularly in handling complex datasets and novel problems. Additionally, we identify concerns with data contamination and memorization, which affect LLM reliability in real-world applications. While OpenAI’s O1 model demonstrates 90% accuracy in reasoning and final answers on complex tasks, it still remains weak in mistake detection. Our findings highlight the need for improved reasoning evaluations and suggest ways to enhance LLM generalization and robustness in math problem-solving.

大型语言模型（LLMs）在数学应用题（MWPs）领域产生了显著影响，改变了这些问题的解决方式，特别是在教育环境中。然而，现有的评估通常侧重于最终准确性，忽视了推理能力这一关键方面。本研究通过评估LLMs检测和纠正推理错误的能力来填补这一空白。我们提出了一个新颖的数据集，MWP-MISTAKE，包含通过基于规则的方法和较小语言模型生成的正确和错误推理步骤的MWPs。我们对GPT-4o和GPT4等最先进模型进行了全面基准测试，揭示了它们的优势和局限性。尽管GPT-4o在错误检测和纠正方面表现出色，但在处理复杂数据集和新问题方面仍存在差距。此外，我们发现了数据污染和记忆化的问题，这些问题影响了LLM在实际应用中的可靠性。虽然OpenAI的O1模型在复杂任务中的推理和最终答案准确率达到90%，但在错误检测方面仍然较弱。我们的研究结果强调了改进推理评估的必要性，并提出了增强LLM在数学问题解决中泛化和鲁棒性的方法。

大型语言模型（LLMs）在数学应用题（MWPs）领域产生了显著影响，改变了这些问题的解决方式，尤其是在教育环境中。然而，现有的评估通常只关注最终准确性，忽视了推理能力这一关键方面。本研究通过评估LLMs检测和纠正推理错误的能力，填补了这一空白。我们提出了一个新颖的数据集MWP-MISTAKE，包含通过规则方法和较小语言模型生成的正确和错误推理步骤的数学应用题。我们对GPT-4o和GPT4等最先进模型的全面基准测试揭示了它们的优势和局限性。尽管GPT-4o在错误检测和纠正方面表现出色，但在处理复杂数据集和新问题时仍存在差距。此外，我们还发现了数据污染和记忆化问题，这影响了LLMs在实际应用中的可靠性。尽管OpenAI的O1模型在复杂任务上的推理和最终答案准确率达到90%，但在错误检测方面仍然薄弱。我们的发现强调了改进推理评估的必要性，并提出了增强LLMs在数学问题解决中泛化和鲁棒性的方法。

48. CS-Bench: A Comprehensive Benchmark for Large Language Models towards Computer Science Mastery

基本信息

标题

CS-Bench: 计算机科学领域大型语言模型的综合基准

CS-Bench: 评估大型语言模型在计算机科学领域掌握程度的综合基准

核心思想

引入多语言基准 CS-Bench 评估 LLMs 在计算机科学领域的全面表现，揭示模型性能与规模的关系，并提出改进方向。

提出CS-Bench基准，全面评估大型语言模型在计算机科学领域的表现，揭示其与模型规模及数学、编码能力的关系，并指出改进方向。

摘要

Computer Science (CS) stands as a testament to the intricacies of human intelligence, profoundly advancing the development of artificial intelligence and modern society. However, the current community of large language models (LLMs) overly focuses on benchmarks for analyzing specific foundational skills (e.g. mathematics and code generation), neglecting an all-round evaluation of the computer science field. To bridge this gap, we introduce CS-Bench, the first multilingual (English, Chinese, French, German) benchmark dedicated to evaluating the performance of LLMs in computer science. CS-Bench comprises approximately 10K meticulously curated test samples, covering 26 subfields across 4 key areas of computer science, encompassing various task forms and divisions of knowledge and reasoning. Utilizing CS-Bench, we conduct a comprehensive evaluation of over 30 mainstream LLMs, revealing the relationship between CS performance and model scales. We also quantitatively analyze the reasons for failures in existing LLMs and highlight directions for improvements, including knowledge supplementation and CS-specific reasoning. Further cross-capability experiments show a high correlation between LLMs’ capabilities in computer science and their abilities in mathematics and coding. Moreover, expert LLMs specialized in mathematics and coding also demonstrate strong performances in several CS subfields. Looking ahead, we envision CS-Bench serving as a cornerstone for LLM applications in the CS field and paving new avenues in assessing LLMs’ diverse reasoning capabilities.

计算机科学 (CS) 展示了人类智能的复杂性，极大地推动了人工智能和现代社会的发展。然而，当前的大型语言模型 (LLMs) 社区过于关注分析特定基础技能 (如数学和代码生成) 的基准，忽视了对计算机科学领域的全面评估。为了填补这一空白，我们引入了 CS-Bench，这是首个专注于评估 LLMs 在计算机科学领域表现的多语言 (英语、中文、法语、德语) 基准。CS-Bench 包含约 10K 个精心挑选的测试样本，涵盖计算机科学的 4 个关键领域中的 26 个子领域，包括各种任务形式和知识与推理的划分。利用 CS-Bench，我们对超过 30 个主流 LLMs 进行了全面评估，揭示了 CS 表现与模型规模之间的关系。我们还定量分析了现有 LLMs 失败的原因，并指出了改进方向，包括知识补充和计算机科学特定的推理。进一步的跨能力实验显示，LLMs 在计算机科学方面的能力与其在数学和编码方面的能力高度相关。此外，在数学和编码方面表现优异的专家 LLMs 在多个 CS 子领域也表现出色。展望未来，我们设想 CS-Bench 将成为 LLM 在 CS 领域应用的基石，并为评估 LLMs 的多样化推理能力开辟新途径。

计算机科学（Computer Science, CS）是人类智慧的复杂体现，深刻推动了人工智能和现代社会的发展。然而，当前大型语言模型（LLMs）社区过度关注分析特定基础技能（如数学和代码生成）的基准，忽视了计算机科学领域的全面评估。为填补这一空白，我们引入了CS-Bench，这是首个多语言（英语、中文、法语、德语）的基准，专门用于评估LLMs在计算机科学中的表现。CS-Bench包含约10,000个精心挑选的测试样本，覆盖计算机科学的4个关键领域中的26个子领域，涵盖多种任务形式和知识与推理的划分。利用CS-Bench，我们对超过30个主流LLMs进行了全面评估，揭示了CS表现与模型规模之间的关系。我们还定量分析了现有LLMs失败的原因，并指出了改进方向，包括知识补充和CS特定推理。进一步的跨能力实验显示，LLMs在计算机科学中的能力与其在数学和编码中的能力高度相关。此外，专长于数学和编码的专家LLMs在多个CS子领域也表现出色。展望未来，我们期望CS-Bench成为LLMs在CS领域应用的基石，并开辟评估LLMs多样化推理能力的新途径。

51. Can I Understand What I Create? Self-Knowledge Evaluation of Large Language Models

基本信息

标题

我能理解我所创造的吗？大型语言模型的自我知识评估

我能否理解我所创造的内容？大型语言模型的自知能力评估

核心思想

引入自我知识评估框架，通过模型自我生成的问题来评估其理解和回应能力，揭示模型在自我知识方面的不足，并提出改进方法。

通过自生成问题评估大型语言模型的自知能力，发现其与人类注意力机制的不匹配，并探讨微调对模型性能的提升作用。

摘要

Large language models (LLMs) have achieved remarkable progress in linguistic tasks, necessitating robust evaluation frameworks to understand their capabilities and limitations. Inspired by Feynman’s principle of understanding through creation, we introduce a self-knowledge evaluation framework that is easy to implement, evaluating models on their ability to comprehend and respond to self-generated questions. Our findings, based on testing multiple models across diverse tasks, reveal significant gaps in the model’s self-knowledge ability. Further analysis indicates these gaps may be due to misalignment with human attention mechanisms. Additionally, fine-tuning on self-generated math task may enhance the model’s math performance, highlighting the potential of the framework for efficient and insightful model evaluation and may also contribute to the improvement of LLMs.

大型语言模型（LLMs）在语言任务中取得了显著进展，需要强大的评估框架来理解其能力和局限性。受费曼通过创造来理解的原理启发，我们引入了一个易于实施的自我知识评估框架，评估模型在理解和回应自身生成问题方面的能力。基于对多个模型在不同任务上的测试，我们的研究结果揭示了模型在自我知识能力方面存在显著差距。进一步分析表明，这些差距可能源于与人类注意力机制的不匹配。此外，对自我生成的数学任务进行微调可能会提高模型的数学表现，突显了该框架在高效且有洞察力的模型评估中的潜力，并可能有助于改进LLMs。

大型语言模型（LLMs）在语言任务中取得了显著进展，这需要强大的评估框架来理解它们的能力和局限性。受费曼通过创造来理解的原则启发，我们引入了一个易于实现的自知能力评估框架，评估模型在理解和回应自生成问题方面的能力。通过对多个模型在不同任务上的测试，我们发现模型在自知能力方面存在显著差距。进一步分析表明，这些差距可能是由于与人类注意力机制的不匹配所致。此外，在自生成的数学任务上进行微调可能会提高模型的数学表现，这突显了该框架在高效且有洞察力的模型评估中的潜力，也可能有助于提升LLMs的性能。

62. JudgeBench: A Benchmark for Evaluating LLM-Based Judges

基本信息

标题

Judge Bench: 一个评估基于 LLM 的评判系统的基准

JudgeBench: 用于评估基于大型语言模型（LLM）的评判器的基准

核心思想

提出 Judge Bench 基准，用于评估基于 LLM 的评判系统在复杂任务中的表现。

提出JudgeBench基准，用于客观评估基于LLM的评判器在复杂任务中的表现，揭示现有模型的不足。

摘要

LLM-based judges have emerged as a scalable alternative to human evaluation and are increasingly used to assess, compare, and improve models. However, the reliability of LLM-based judges themselves is rarely scrutinized. As LLMs become more advanced, their responses grow more sophisticated, requiring stronger judges to evaluate them. Existing benchmarks primarily focus on a judge’s alignment with human preferences, but often fail to account for more challenging tasks where crowdsourced human preference is a poor indicator of factual and logical correctness. To address this, we propose a novel evaluation framework to objectively evaluate LLM-based judges. Based on this framework, we propose JudgeBench, a benchmark for evaluating LLM-based judges on challenging response pairs spanning knowledge, reasoning, math, and coding. JudgeBench leverages a novel pipeline for converting existing difficult datasets into challenging response pairs with preference labels reflecting objective correctness. Our comprehensive evaluation on a collection of prompted judges, fine-tuned judges, multi-agent judges, and reward models shows that JudgeBench poses a significantly greater challenge than previous benchmarks, with many strong models (e.g. GPT-4o) performing just slightly better than random guessing. Overall, JudgeBench offers a reliable platform for assessing increasingly advanced LLM-based judges. Data and code are available at \url{https://anonymous.4open.science/r/JudgeBench-ICLR2025/}.

基于 LLM 的评判系统作为一种可扩展的人类评估替代方案，正越来越多地用于评估、比较和改进模型。然而，这些基于 LLM 的评判系统本身的可靠性却很少受到审查。随着 LLM 的进步，它们的响应变得更加复杂，需要更强的评判系统来评估它们。现有的基准主要关注评判系统与人类偏好的对齐，但往往未能考虑到更复杂的任务，在这些任务中，众包的人类偏好并不能很好地指示事实和逻辑的正确性。为了解决这一问题，我们提出了一种新的评估框架，以客观地评估基于 LLM 的评判系统。基于此框架，我们提出了 Judge Bench，这是一个用于评估基于 LLM 的评判系统在涵盖知识、推理、数学和编码的挑战性响应对上的基准。Judge Bench 利用一种新颖的流程，将现有的困难数据集转换为具有反映客观正确性的偏好标签的挑战性响应对。我们对一系列提示评判系统、微调评判系统、多代理评判系统和奖励模型进行了全面的评估，结果显示 Judge Bench 比之前的基准提出了更大的挑战，许多强模型（例如 GPT-4o）的表现仅略好于随机猜测。总的来说，Judge Bench 提供了一个可靠的平台，用于评估日益先进的基于 LLM 的评判系统。数据和代码可在 \url{https://anonymous.4open.science/r/JudgeBench-ICLR2025/} 获取。

基于大型语言模型（LLM）的评判器作为一种可扩展的替代人类评估的方法，正越来越多地被用于评估、比较和改进模型。然而，LLM-based评判器本身的可靠性却很少受到审视。随着LLM技术的不断进步，其生成的响应也变得更加复杂，这要求更强大的评判器来对其进行评估。现有的基准主要关注评判器与人类偏好的契合度，但往往未能涵盖更具挑战性的任务，在这些任务中，众包的人类偏好并不能很好地反映事实和逻辑的正确性。为了解决这一问题，我们提出了一个新颖的评估框架，用于客观地评估基于LLM的评判器。基于此框架，我们提出了JudgeBench，这是一个用于评估LLM-based评判器在知识、推理、数学和编程等挑战性响应对上的基准。JudgeBench利用一种新颖的流程，将现有的困难数据集转换为具有反映客观正确性偏好标签的挑战性响应对。我们对一系列提示型评判器、微调型评判器、多代理评判器和奖励模型进行了全面评估，结果显示JudgeBench比之前的基准提出了显著更大的挑战，许多强大的模型（例如GPT-4o）的表现仅略优于随机猜测。总体而言，JudgeBench为评估日益先进的基于LLM的评判器提供了一个可靠的平台。数据和代码可在\url{https://anonymous.4open.science/r/JudgeBench-ICLR2025/}获取。

64. MathEval: A Comprehensive Benchmark for Evaluating Large Language Models on Mathematical Reasoning Capabilities

基本信息

标题

MathEval: 一个全面评估大型语言模型数学推理能力的基准

MathEval: 用于评估大型语言模型数学推理能力的综合基准

核心思想

引入 MathEval 基准，全面评估 LLMs 的数学推理能力，并解决数据污染问题。

提出MathEval综合基准，系统评估大型语言模型的数学推理能力，并识别预训练数据污染。

摘要

Mathematical reasoning is a fundamental aspect of intelligence, encompassing a spectrum from basic arithmetic to intricate problem-solving. Recent investigations into the mathematical abilities of large language models (LLMs) have yielded inconsistent and incomplete assessments. In response, we introduce MathEval, a comprehensive benchmark designed to methodically evaluate the mathematical problem-solving proficiency of LLMs across varied contexts, adaptation strategies, and evaluation metrics. MathEval amalgamates 19 datasets, spanning an array of mathematical domains, languages, problem types, and difficulty levels, from elementary to advanced. This diverse collection facilitates a thorough appraisal of LLM performance and is stratified by language (English and Chinese), problem category (arithmetic, competitive mathematics, and higher mathematics), and difficulty. To overcome the challenges of standardizing responses across diverse models and prompts, we’ve developed an automated LLM-driven pipeline for answer extraction and comparison, ensuring consistent evaluation criteria. To broaden the utility of MathEval beyond the scope of GPT-4, we have harnessed the extensive results from GPT-4 to train a deepseek-7B-based answer comparison model, enabling precise answer validation for those without access to GPT-4. This model will also be made publicly available. MathEval not only assesses mathematical proficiency but also introduces a method to identify potential data contamination within pre-training datasets. This is done by hypothesizing that enhancements in one mathematical dataset should be mirrored by advancements in correlated datasets, thus signaling potential contamination—like the inadvertent inclusion of test data in the pre-training phase. To mitigate this and truly gauge progress, MathEval incorporates an annually refreshed set of problems from the latest Chinese National College Entrance Examination (Gaokao 2023), thereby benchmarking genuine advancements in mathematical problem solving skills. MathEval strives to refine the assessment of Large Language Models’ (LLMs) capabilities in mathematics.

数学推理是智能的一个基本方面，涵盖了从基本算术到复杂问题解决的广泛范围。最近对大型语言模型（LLMs）数学能力的研究产生了不一致和不完整的评估结果。为此，我们引入了 MathEval，这是一个全面的基准，旨在系统地评估 LLMs 在各种情境、适应策略和评估指标下的数学问题解决能力。MathEval 整合了 19 个数据集，涵盖了从基础到高级的多种数学领域、语言、问题类型和难度级别。这种多样化的集合有助于全面评估 LLM 的表现，并按语言（英语和中文）、问题类别（算术、竞赛数学和高数）和难度进行分层。为了克服不同模型和提示之间标准化响应的挑战，我们开发了一个自动化的 LLM 驱动的答案提取和比较管道，确保一致的评估标准。为了扩大 MathEval 的实用性，超越 GPT-4 的范围，我们利用 GPT-4 的广泛结果训练了一个基于 deepseek-7B 的答案比较模型，使得那些无法访问 GPT-4 的用户也能进行精确的答案验证。该模型也将公开发布。MathEval 不仅评估数学能力，还引入了一种方法来识别预训练数据集中的潜在数据污染。这是通过假设一个数学数据集的改进应反映在相关数据集的进展中，从而表明潜在的污染——例如在预训练阶段无意中包含了测试数据。为了缓解这一问题并真正衡量进展，MathEval 包含了来自最新中国高考（2023 年高考）的年度更新的问题集，从而基准化数学问题解决技能的真正进步。MathEval 致力于完善对大型语言模型（LLMs）数学能力的评估。

数学推理是智能的基本方面，涵盖从基础算术到复杂问题解决的广泛范围。近期对大型语言模型（LLMs）数学能力的研究结果不一致且不完整。为此，我们提出了MathEval，这是一个旨在系统评估LLMs在不同情境、适应策略和评估指标下数学问题解决能力的综合基准。MathEval整合了19个数据集，覆盖了多种数学领域、语言、问题类型和难度级别，从初级到高级。这一多样化集合有助于全面评估LLMs的表现，并按语言（英语和中文）、问题类别（算术、竞赛数学和高等数学）和难度进行分层。为了克服在多样化模型和提示中标准化响应的挑战，我们开发了一个自动化的、由LLM驱动的答案提取和比较流程，确保评估标准的一致性。为了扩展MathEval在GPT-4范围之外的应用，我们利用GPT-4的广泛结果训练了一个基于deepseek-7B的答案比较模型，使那些无法访问GPT-4的用户也能进行精确的答案验证。该模型也将公开提供。MathEval不仅评估数学能力，还引入了一种方法来识别预训练数据集中的潜在数据污染。这是通过假设在一个数学数据集上的改进应在相关数据集中得到反映，从而指示潜在的污染——如无意中将测试数据包含在预训练阶段。为了真正衡量进展，MathEval还纳入了每年更新的最新中国全国高考（Gaokao 2023）问题集，从而基准测试数学问题解决技能的真实进步。MathEval致力于精细化评估大型语言模型（LLMs）在数学方面的能力。

65. Navigating the Labyrinth: Evaluating and Enhancing LLMs’ Ability to Reason About Search Problems

基本信息

标题

探索迷宫：评估和增强大型语言模型在搜索问题上的推理能力

导航迷宫：评估和提升大型语言模型在搜索问题上的推理能力

核心思想

引入SearchBench基准测试和基于A*算法的多阶段推理方法，显著提升大型语言模型在复杂搜索问题上的表现。

引入新的组合问题基准测试，揭示大型语言模型在多步推理上的不足，并提出基于A*算法的提示和推理方法显著提升模型性能。

摘要

Recently, Large Language Models (LLMs) attained impressive performance in math and reasoning benchmarks. However, they still often struggle with multi-step reasoning which is relatively easy for humans. To further investigate this, we introduce a new benchmark, SearchBench, containing 11 unique combinatorial problems that avoid training contamination (each equipped with automated pipelines to generate an arbitrary number of instances) and analyze the feasibility, correctness, and optimality of LLM-generated solutions. We show that even the most advanced LLMs fail to solve these problems end-to-end in text, e.g., GPT4 and o1-preview respectively solve only 1.4% and 18.6% correctly. SearchBench problems require considering multiple pathways to the solution and backtracking, posing a significant challenge to auto-regressive models. Instructing LLMs to generate code that solves the problem helps only slightly. We next introduce an in-context learning approach that prompts the model to implement A*, an informed search algorithm, to comprehensively traverse the problem state space, improving the performance of models. We further extend this approach and propose the Multi-Stage-Multi-Try inference method which breaks down the A* algorithm implementation into two stages and auto-verifies the first stage against unit tests, raising GPT-4’s performance above 57%.

最近，大型语言模型（LLMs）在数学和推理基准测试中取得了令人印象深刻的性能。然而，它们在多步骤推理方面仍然经常遇到困难，这对人类来说相对容易。为了进一步研究这一点，我们引入了一个新的基准测试，SearchBench，包含11个独特的组合问题，避免了训练污染（每个问题都配备了自动化的管道来生成任意数量的实例），并分析了LLM生成解决方案的可行性、正确性和最优性。我们展示了即使是最高级的LLMs也无法在文本中端到端地解决这些问题，例如，GPT4和o1-preview分别仅能正确解决1.4%和18.6%的问题。SearchBench问题需要考虑多条通向解决方案的路径和回溯，这对自回归模型构成了重大挑战。指导LLMs生成解决问题的代码只能稍微有所帮助。接下来，我们引入了一种上下文学习方法，提示模型实现A*，一种启发式搜索算法，以全面遍历问题状态空间，从而提高模型的性能。我们进一步扩展了这种方法，并提出了多阶段多尝试推理方法，将A*算法的实现分解为两个阶段，并自动验证第一阶段对单元测试的符合性，使GPT-4的性能提升至57%以上。

近期，大型语言模型（LLMs）在数学和推理基准测试中取得了令人瞩目的表现。然而，它们在多步推理任务上仍然常常遇到困难，而这些任务对人类来说相对简单。为了进一步探究这一问题，研究者引入了一个新的基准测试，名为SearchBench，包含11个独特的组合问题（每个问题都配备了自动化管道以生成任意数量的实例），以避免训练数据污染，并分析LLM生成解决方案的可行性、正确性和最优性。研究表明，即使是最新的大型语言模型，如GPT-4和o1-preview，在纯文本环境下也难以端到端地解决这些问题，正确率分别仅为1.4%和18.6%。SearchBench问题需要考虑多种路径和回溯，对自回归模型构成了重大挑战。指导LLM生成解决问题的代码仅略有帮助。随后，研究者提出了一种上下文学习方法，提示模型实现A这一启发式搜索算法，以全面遍历问题状态空间，从而提升了模型性能。进一步地，研究者扩展了这一方法，提出了多阶段多尝试推理方法，将A算法实现分为两个阶段，并自动验证第一阶段是否符合单元测试，使GPT-4的性能提升至57%以上。

67. Number Cookbook: Number Understanding of Language Models and How to Improve It

基本信息

标题

数字烹饪书：语言模型对数字的理解及其改进方法

数字食谱：语言模型的数字理解及其改进方法

核心思想

全面研究并改进大型语言模型在数字理解和处理方面的能力。

全面评估和提升大型语言模型的数字理解和处理能力

摘要

Large language models (LLMs) can solve an increasing number of complex tasks while making surprising mistakes in basic numerical understanding and processing (such as 9.11>9.99.11 > 9.9). The latter ability is essential for tackling complex arithmetic and mathematical problems and serves as a foundation for most reasoning tasks, but previous work paid less attention to it or only discussed several restricted tasks (like integer addition). In this paper, we comprehensively investigate the numerical understanding and processing ability (NUPA) of LLMs. Firstly, we introduce a test suite covering four common numerical representations and 17 distinct numerical tasks in four major categories, resulting in 41 meaningful combinations in total. These tasks are derived from primary and secondary education curricula, encompassing nearly all everyday numerical understanding and processing scenarios, and the rules of these tasks are very simple and clear.
We find that current LLMs exhibit a considerable probability of error in many of them. To address this, we analyze and evaluate techniques designed to enhance NUPA, identifying three key factors that influence NUPA of LLMs. We also perform finetuning of practical-scale LLMs on our defined NUPA tasks and find that a naive finetuning improves the performance but these tricks cannot be directly used to finetune an already-trained model. We further explore the impact of chain-of-thought techniques on NUPA. Our work takes an initial step towards understanding and improving NUPA of LLMs.

大型语言模型（LLMs）能够解决越来越多的复杂任务，但在基本的数字理解和处理上却犯下令人惊讶的错误（例如 9.11>9.99.11 > 9.9）。后一种能力对于解决复杂的算术和数学问题至关重要，并且是大多数推理任务的基础，但以往的工作对此关注较少，或者仅讨论了几个受限的任务（如整数加法）。本文全面研究了 LLMs 的数字理解和处理能力（NUPA）。首先，我们引入了一个测试套件，涵盖了四种常见的数字表示和四大类中的 17 个不同的数字任务，总共产生了 41 个有意义的组合。这些任务源自小学和中学教育课程，几乎涵盖了所有日常数字理解和处理的场景，并且这些任务的规则非常简单明了。我们发现，当前的 LLMs 在这些任务中表现出相当大的错误概率。为了解决这个问题，我们分析和评估了旨在增强 NUPA 的技术，确定了影响 LLMs NUPA 的三个关键因素。我们还在我们定义的 NUPA 任务上对实际规模的 LLMs 进行了微调，发现简单的微调可以提高性能，但这些技巧不能直接用于微调已经训练好的模型。我们进一步探讨了思维链技术对 NUPA 的影响。我们的工作迈出了理解和改进 LLMs NUPA 的第一步。

大型语言模型（LLMs）能够解决越来越多的复杂任务，但在基本的数字理解和处理方面（例如 9.11>9.99.11 > 9.9）却会犯令人惊讶的错误。后一种能力对于解决复杂的算术和数学问题至关重要，并且是大多数推理任务的基础，但以往的研究对此关注较少，或者仅讨论了某些受限任务（如整数加法）。在本文中，我们全面研究了LLMs的数字理解和处理能力（NUPA）。首先，我们引入了一个测试套件，涵盖四种常见的数字表示和四大类中的17个不同数字任务，总共形成41种有意义的组合。这些任务源自中小学教育课程，涵盖了几乎所有日常数字理解和处理场景，且这些任务的规则非常简单明了。我们发现，当前LLMs在许多任务中存在相当高的错误概率。为解决这一问题，我们分析和评估了旨在提升NUPA的技术，识别出影响LLMs NUPA的三个关键因素。我们还对实用规模的LLMs进行了针对我们定义的NUPA任务的微调，发现简单的微调可以提升性能，但这些技巧不能直接用于微调已训练模型。我们进一步探讨了思维链技术对NUPA的影响。我们的工作为理解和提升LLMs的NUPA迈出了初步的一步。

68. Unearthing Large Scale Domain-Specific Knowledge from Public Corpora

基本信息

标题

从公共语料库中挖掘大规模特定领域知识

从公共语料库中挖掘大规模领域特定知识

核心思想

利用大型语言模型从公共语料库中自动检索和生成特定领域知识。

利用大型模型从公共语料库中自动挖掘和检索特定领域的知识数据，提升领域特定任务的性能。

摘要

Large language models (LLMs) have demonstrated remarkable potential in various tasks, however, there remains a significant lack of open-source models and data for specific domains. Previous work has primarily focused on manually specifying resources and collecting high-quality data for specific domains, which is extremely time-consuming and labor-intensive. To address this limitation, we introduce large models into the data collection pipeline to guide the generation of domain-specific information and retrieve relevant data from Common Crawl (CC), a large public corpus. We refer to this approach as Retrieve-from-CC. It not only collects data related to domain-specific knowledge but also mines the data containing potential reasoning procedures from the public corpus. By applying this method, we have collected a knowledge domain-related dataset named Retrieve-Pile, which covers four main domains, including the sciences, humanities, and other categories. Through the analysis of Retrieve-Pile, Retrieve-from-CC can effectively retrieve relevant data from the covered knowledge domains and significantly improve the performance in tests of mathematical and knowledge-related reasoning abilities.

大型语言模型（LLMs）在各种任务中展示了显著的潜力，然而，特定领域的开源模型和数据仍然严重缺乏。以往的工作主要集中在手动指定资源和收集特定领域的高质量数据，这非常耗时且劳动密集。为了解决这一限制，我们将大型模型引入数据收集流程，以指导特定领域信息的生成，并从 Common Crawl（CC）这一大型公共语料库中检索相关数据。我们将这种方法称为 Retrieve-from-CC。它不仅收集与特定领域知识相关的数据，还从公共语料库中挖掘包含潜在推理过程的数据。通过应用这种方法，我们收集了一个名为 Retrieve-Pile 的知识领域相关数据集，涵盖了科学、人文和其他四个主要领域。通过对 Retrieve-Pile 的分析，Retrieve-from-CC 能够有效地从所涵盖的知识领域中检索相关数据，并显著提高数学和知识相关推理能力测试中的表现。

大型语言模型（LLMs）在各类任务中展现出显著潜力，然而，特定领域的开源模型和数据仍然严重缺乏。先前的研究主要依赖于手动指定资源和收集特定领域的高质量数据，这一过程极为耗时且劳动密集。为克服这一局限，我们将大型模型引入数据收集流程，以指导生成领域特定信息，并从大型公共语料库Common Crawl（CC）中检索相关数据。我们将这种方法称为Retrieve-from-CC。该方法不仅收集与领域特定知识相关的数据，还从公共语料库中挖掘包含潜在推理过程的数据。通过应用此方法，我们收集了一个名为Retrieve-Pile的知识领域相关数据集，涵盖科学、人文及其他类别等四个主要领域。通过对Retrieve-Pile的分析，Retrieve-from-CC能够有效从覆盖的知识领域中检索相关数据，并在数学和知识相关推理能力的测试中显著提升性能。

73. How to Get Your LLM to Generate Challenging Problems for Evaluation

基本信息

标题

如何让 LLM 生成用于评估的挑战性问题

如何让大型语言模型生成具有挑战性的问题以进行评估

核心思想

提出一个无需人工干预的框架 CHASE，用于合成生成挑战性问题以评估 LLMs。

提出CHASE框架，利用LLMs自动生成具有挑战性的问题以评估模型性能

摘要

The pace of evolution of Large Language Models (LLMs) necessitates new approaches for rigorous and comprehensive evaluation. Traditional human annotation is increasingly impracticable due to the complexities and costs involved in generating high-quality, challenging problems, particularly for tasks such as long-context reasoning. Moreover, the rapid saturation of existing human-curated benchmarks by LLMs further necessitates the need to develop scalable and automatically renewable evaluation methodologies. In this work, we introduce CHASE, a unified framework to synthetically generate challenging problems using LLMs without human involvement. For a given task, our approach builds a hard problem in a bottom-up manner from simpler components. Moreover since we want to generate synthetic data for evaluation, our framework decomposes the generation process into independently verifiable sub-tasks, thereby ensuring a high level of quality and correctness. We implement CHASE to create evaluation benchmarks across three diverse domains: document-based question answering, repository-level code completion, and math reasoning. The performance of state-of-the-art LLMs on these synthetic benchmarks lies in the range of 40-60% accuracy, thereby demonstrating the effectiveness of our framework at generating hard problems. Our experiments further reveal that the Gemini models significantly outperform other LLMs at long-context reasoning, and that the performance of all LLMs drastically drops by as much as 70% when we scale up the context size to 50k tokens.

大型语言模型（LLMs）的快速发展需要新的严格和全面评估方法。由于生成高质量、具有挑战性问题的复杂性和成本，传统的人工标注越来越不切实际，特别是在长上下文推理等任务中。此外，现有的人工策划基准的快速饱和进一步需要开发可扩展和自动更新的评估方法。在这项工作中，我们介绍了 CHASE，一个无需人工干预即可合成生成挑战性问题的统一框架。对于给定的任务，我们的方法从简单的组件逐步构建出难题。此外，由于我们希望生成用于评估的合成数据，我们的框架将生成过程分解为可独立验证的子任务，从而确保高质量和正确性。我们实现了 CHASE，以在三个不同领域创建评估基准：基于文档的问答、仓库级别的代码补全和数学推理。在这些合成基准上，最先进的 LLMs 的性能准确率在 40-60% 之间，从而证明了我们框架在生成难题方面的有效性。我们的实验进一步揭示，Gemini 模型在长上下文推理方面显著优于其他 LLMs，并且当我们将上下文大小扩展到 50k 个标记时，所有 LLMs 的性能急剧下降了高达 70%。

随着大型语言模型（LLMs）的快速发展，迫切需要新的方法来进行严格和全面的评估。传统的人工标注由于生成高质量、具有挑战性问题的复杂性和成本，尤其是对于长上下文推理等任务，变得越来越不切实际。此外，现有的人工策划基准被LLMs迅速饱和，进一步需要开发可扩展和自动更新的评估方法。在这项工作中，我们介绍了CHASE，一个无需人工参与，利用LLMs合成生成具有挑战性问题的统一框架。对于给定任务，我们的方法从更简单的组件以自下而上的方式构建难题。此外，由于我们希望生成用于评估的合成数据，我们的框架将生成过程分解为可独立验证的子任务，从而确保高水平的质量和正确性。我们实现了CHASE，在三个不同领域创建了评估基准：基于文档的问题回答、仓库级别的代码补全和数学推理。最先进LLMs在这些合成基准上的表现 accuracy 范围在40-60%，从而证明了我们框架在生成难题方面的有效性。我们的实验进一步揭示，Gemini模型在长上下文推理方面显著优于其他LLMs，并且当我们将上下文大小扩展到50k tokens时，所有LLMs的性能急剧下降，降幅高达70%。

75. Evaluating Robustness of Reward Models for Mathematical Reasoning

基本信息

  • 论文地址：Evaluating Robustness of Reward Models for Mathematical Reasoning
  • 关键词：mathematical reasoning, RLHF, reward models, reward overoptimization, language models, benchmark
  • 领域：datasets and benchmarks
  • TLDR: We propose a design for a reliable benchmark for reward models and validate our design using the results of optimized policies and through the lens of reward overoptimization.

标题

评估数学推理中奖励模型的鲁棒性

评估数学推理奖励模型的鲁棒性

核心思想

提出新的设计以可靠评估奖励模型的鲁棒性，并通过RewardMATH基准验证。

提出一种可靠评估奖励模型的新设计，并通过RewardMATH基准验证其有效性，以提高评估的可靠性和奖励模型的鲁棒性。

摘要

Reward models are key in reinforcement learning from human feedback (RLHF) systems, aligning the model behavior with human preferences.
Particularly in the math domain, there have been plenty of studies using reward models to align policies for improving reasoning capabilities.
Recently, as the importance of reward models has been emphasized, RewardBench is proposed to understand their behavior.
However, we figure out that the math subset of RewardBench has different representations between chosen and rejected completions, and relies on a single comparison, which may lead to unreliable results as it only see an isolated case.
Therefore, it fails to accurately present the robustness of reward models, leading to a misunderstanding of its performance and potentially resulting in reward hacking.
In this work, we introduce a new design for reliable evaluation of reward models, and to validate this, we construct RewardMATH, a benchmark that effectively represents the robustness of reward models in mathematical reasoning tasks.
We demonstrate that the scores on RewardMATH strongly correlate with the results of optimized policy and effectively estimate reward overoptimization, whereas the existing benchmark shows almost no correlation.
The results underscore the potential of our design to enhance the reliability of evaluation, and represent the robustness of reward model.
We make our code and data publicly available.

奖励模型在从人类反馈中进行强化学习（RLHF）系统中起着关键作用，使模型行为与人类偏好保持一致。特别是在数学领域，已有大量研究使用奖励模型来调整策略以提高推理能力。最近，随着奖励模型的重要性被强调，提出了RewardBench以理解其行为。然而，我们发现RewardBench的数学子集在选定和拒绝的完成之间具有不同的表示，并且依赖于单一比较，这可能导致结果不可靠，因为它只看到一个孤立的案例。因此，它无法准确呈现奖励模型的鲁棒性，导致对其性能的误解，并可能引发奖励操纵。在这项工作中，我们引入了一种新的设计，用于可靠地评估奖励模型，并通过构建RewardMATH基准来验证这一点，该基准有效地代表了奖励模型在数学推理任务中的鲁棒性。我们证明，RewardMATH的得分与优化策略的结果高度相关，并能有效估计奖励过度优化，而现有的基准几乎没有相关性。结果强调了我们的设计增强评估可靠性的潜力，并代表了奖励模型的鲁棒性。我们公开了我们的代码和数据。

奖励模型在基于人类反馈的强化学习（RLHF）系统中至关重要，它们使模型行为与人类偏好保持一致。特别是在数学领域，已有大量研究使用奖励模型来调整策略，以提高推理能力。近期，随着奖励模型重要性的凸显，RewardBench被提出用于理解其行为。然而，我们发现RewardBench的数学子集在选择和拒绝的补全之间存在不同的表示，且依赖于单一比较，这可能导致不可靠的结果，因为它只看到一个孤立的案例。因此，它无法准确呈现奖励模型的鲁棒性，导致对其性能的误解，并可能引发奖励操纵。在这项工作中，我们引入了一种新的设计，用于可靠地评估奖励模型，并为此构建了RewardMATH，一个有效表示数学推理任务中奖励模型鲁棒性的基准。我们证明，RewardMATH上的分数与优化策略的结果高度相关，并能有效估计奖励过优化，而现有基准几乎无相关性。结果表明，我们的设计有潜力提高评估的可靠性，并代表奖励模型的鲁棒性。我们将代码和数据公开可用。

27. BRIGHT: A Realistic and Challenging Benchmark for Reasoning-Intensive Retrieval

基本信息

标题

BRIGHT: 一个现实且具有挑战性的推理密集型检索基准

BRIGHT: 一个现实且具有挑战性的推理密集型检索基准

核心思想

引入 BRIGHT 基准，强调复杂查询中推理的重要性，并展示现有模型在此类查询上的不足。

提出BRIGHT基准，用于评估在复杂现实查询中需要密集推理的文本检索系统，并展示通过显式推理和结合检索文档提升性能的方法。

摘要

Existing retrieval benchmarks primarily consist of information-seeking queries (e.g., aggregated questions from search engines) where keyword or semantic-based retrieval is usually sufficient. However, many complex real-world queries require in-depth reasoning to identify relevant documents that go beyond surface form matching. For example, finding documentation for a coding question requires understanding the logic and syntax of the functions involved. To better benchmark retrieval on such challenging queries, we introduce BRIGHT, the first text retrieval benchmark that requires intensive reasoning to retrieve relevant documents. Our dataset consists of 1,398 real-world queries spanning diverse domains such as economics, psychology, mathematics, coding, and more. These queries are drawn from naturally occurring or carefully curated human data. Extensive evaluation reveals that even state-of-the-art retrieval models perform poorly on BRIGHT. The leading model on the MTEB leaderboard (Muennighoff et al., 2023), which achieves a score of 59.0 nDCG@10,1 produces a score of nDCG@10 of 18.0 on BRIGHT. We show that incorporating explicit reasoning about the query improves retrieval performance by up to 12.2 points. Moreover, incorporating retrieved documents from the top-performing retriever boosts question answering performance by over 6.6 points. We believe that BRIGHT paves the way for future research on retrieval systems in more realistic and challenging settings.

现有的检索基准主要由信息寻求查询（例如，从搜索引擎汇总的问题）组成，其中基于关键词或语义的检索通常已足够。然而，许多复杂的现实世界查询需要深入的推理来识别超越表面形式匹配的相关文档。例如，查找编码问题的文档需要理解涉及的逻辑和语法。为了更好地在如此具有挑战性的查询上进行检索基准测试，我们引入了 BRIGHT，这是第一个需要密集推理来检索相关文档的文本检索基准。我们的数据集包含 1,398 个来自经济学、心理学、数学、编码等多个领域的真实世界查询。这些查询来自自然发生或精心策划的人类数据。广泛的评估显示，即使是目前最先进的检索模型在 BRIGHT 上也表现不佳。在 MTEB 排行榜上领先的模型（Muennighoff 等人，2023 年），其 nDCG@10 得分为 59.0，在 BRIGHT 上的 nDCG@10 得分为 18.0。我们表明，对查询进行显式推理可以提高检索性能高达 12.2 分。此外，结合顶级检索器的检索文档可以提高问答性能超过 6.6 分。我们相信 BRIGHT 为未来在更现实和更具挑战性的环境中研究检索系统铺平了道路。

现有的检索基准主要包含信息寻求型查询（例如，来自搜索引擎的聚合问题），在这些查询中，基于关键词或语义的检索通常已足够。然而，许多复杂的现实世界查询需要深入推理才能识别出与表面形式匹配之外的相关文档。例如，查找编码问题的文档需要理解所涉及函数的逻辑和语法。为了更好地在这些具有挑战性的查询上评估检索效果，我们引入了BRIGHT，这是第一个需要密集推理才能检索到相关文档的文本检索基准。我们的数据集包含1,398个现实世界查询，涵盖经济学、心理学、数学、编码等多个领域。这些查询来自自然发生或精心策划的人类数据。广泛的评估显示，即使是当前最先进的检索模型在BRIGHT上的表现也较差。MTEB排行榜上的领先模型（Muennighoff等人，2023年），在MTEB上获得59.0的nDCG@10得分，而在BRIGHT上仅为18.0。我们表明，通过对查询进行显式推理，可以提升检索性能高达12.2分。此外，结合来自表现最佳的检索器的检索文档，可以将问答性能提升超过6.6分。我们相信，BRIGHT为未来在更现实和具有挑战性的设置中进行检索系统研究铺平了道路。