Blueprint 技术指南 | 构建数学协作新生态
数学形式化的新挑战
在当代数学研究中,一个完整的证明可能横跨数百页技术细节,但即使是最杰出的数学家也难免在冗长的证明中出现疏漏。这使得传统的同行评议机制难以全面把控证明的正确性。在这样的背景下,Blueprint 项目应运而生。它是由法国数学家 Patrick Massot 开发的工具,致力于管理和协调大型形式化数学项目,为数学证明的形式化过程提供了系统性的解决方案。
本文将深索 leanblueprint 的核心特性,通过分析经典项目案例,展示这一工具如何革新数学形式化的工作流程,并通过一个完整的实践示例解释其功能用法。
解析经典项目:以费马大定理为例
我们从 Lean 社区的经典项目 费马大定理入手,了解 Blueprint 是什么,由哪些东西构成。
费马大定理(Fermat’s Last Theorem):对于任意正整数 、、 和大于等于 3 的正整数 ,方程 没有解。这个命题由费马于 1637 年提出,直到 1994 年才被怀尔斯(在泰勒的协助下)最终证明。虽然现在已经出现了几种不同的证明方法,但它们都遵循相似的思路,依赖于椭圆曲线和模形式理论。
这个定理的魅力在于:表述仅涉及初等数学概念,却需要现代数学中最深刻的理论才能完成证明。 Lean 提供了简洁的形式化表述:
1 | /-- 在给定半环上针对特定指数的费马大定理表述 -/ |
虽然表述简洁,但完整的证明需要构建和形式化大量现代数学理论。
FLT 项目
FLT(Fermat’s Last Theorem)项目 是由 Kevin Buzzard 领导,获得英国工程和物理科学研究委员会(EP/Y022904/1)资助的大型形式化项目。
项目网站包括:
-
主文档网站
- 由 Lean 社区的 doc-gen4 工具生成
- 提供完整的 API 文档和代码导航

-
Blueprint 可视化界面
- 通过项目主页的 blueprint 链接访问
- 展示形式化进度和依赖关系

以第二章为例,Blueprint 通过直观的可视化系统来展示项目状态:
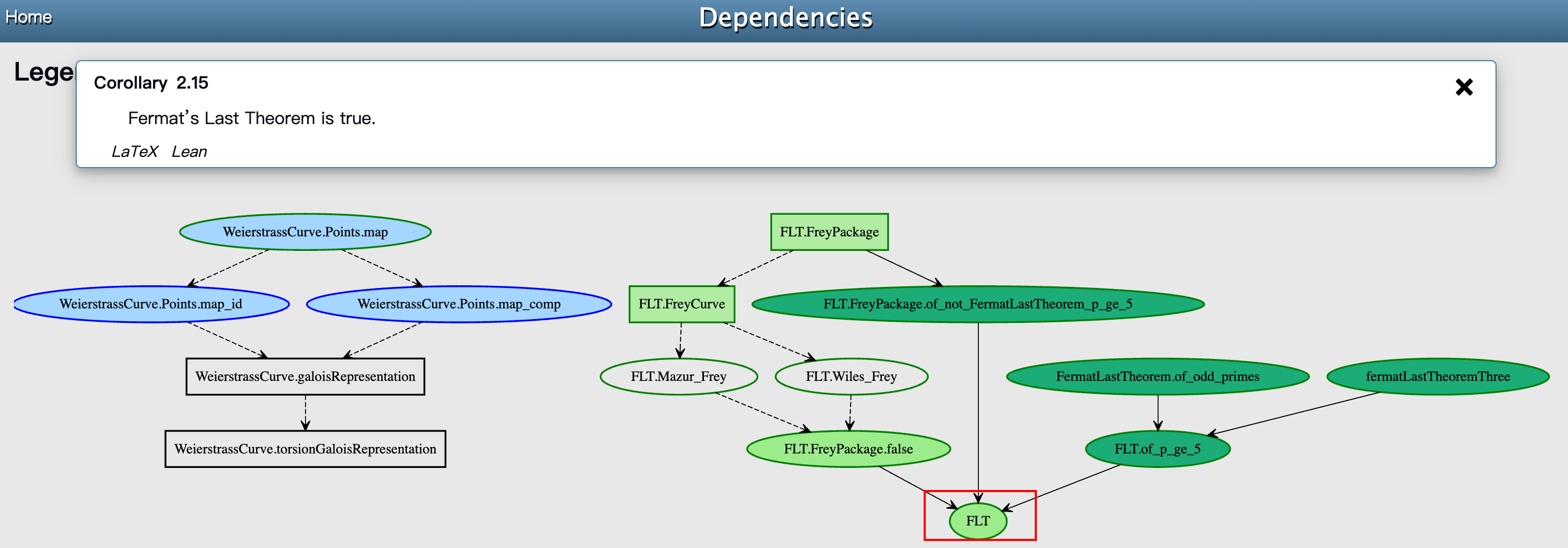
-
节点类型
- 圆形:定理(需要证明的数学陈述)
- 矩形:定义(数学概念的形式化)
- 菱形:引理(辅助性的中间结果)
-
状态颜色编码
- 绿色:完成形式化(stated/proved)
- 蓝色:准备就绪(can_state/can_prove)
- 橙色:未准备就绪(not_ready)
- 深绿色:已并入 mathlib(mathlib)
- 白色绿边:已完成陈述但证明未完成
在正文部分,通过点击引理旁边的链接,也能跳转到对应的 Lean 代码。

部署指南
以下是在 Ubuntu 系统上的完整部署流程:
- 环境准备
1 | # 安装 Lean(如果尚未安装) |
- 项目初始化
1 | # 克隆项目并更新依赖 |
- 生成文档
1 | # 生成所有文档 |
Blueprint 为项目提供三种输出:
-
Web 界面
- 位于
<repo>/blueprint/web - 提供交互式导航和实时更新
- 支持全文搜索功能
- 位于
-
PDF 文档
- 位于
<repo>/blueprint/print/print.pdf - 适合学术交流和存档
- 保持传统数学论文的格式
- 位于
-
API 文档
- 由 doc-gen4 自动生成
- 提供详细的技术实现文档
- 便于开发者理解和使用代码
所有生成的文档都位于 blueprint 目录下,不会影响原有的 Lean 代码。
Blueprint 技术浅析
回到我们的问题。
什么是 Blueprint
leanblueprint 是为 Lean 4 定理证明项目设计的、基于 Python 的命令行工具。其设计理念是将传统数学写作的 LaTeX 工作流与严谨的 Lean 形式化代码无缝结合。
它的主要亮点包括:
- 创建“动态蓝图”:将数学家撰写的 LaTeX 格式的证明大纲(蓝图)与项目中对应的 Lean 代码链接起来。
- 可视化项目进度:自动生成一个交互式的依赖关系图 (Dependency Graph),直观展示项目中每个定义、引理和定理的形式化状态(已完成、进行中或未开始)。
- 自动化文档生成:自动生成内容同步的输出:
- 一份高质量的、适合发表的 PDF 论文。
- 一个功能丰富的交互式静态网站,包含代码 API 文档和动态依赖图。
这些设计让数学家能够在熟悉的 LaTeX 环境中专注于证明构思,而形式化专家则可以专注于代码实现,两者的工作成果通过 Blueprint 实现完美协同。
传统的数学论文写作是线性的、静态的。一旦发表则修改困难,错误可能长期存在。二者相比
| 特性 | 传统方法 | Blueprint 方案 |
|---|---|---|
| 更新机制 | 静态,修改困难 | 动态实时更新 |
| 内容组织 | 线性结构 | 模块化管理 |
| 正确性保证 | 完全人工审核 | 自动形式化验证 |
| 错误处理 | 事后发现 | 实时预防 |
Blueprint 的工作原理
理解 leanblueprint 的关键在于,它不是 Lean 的一部分,而是一个独立于 Lean 构建系统(Lake)之外的、基于 Python 的外部工具。它的工作流程巧妙地利用了成熟的 TeX 生态和脚本能力。
其主要包含了以下几个部分:
- 解析 LaTeX:
leanblueprint的核心依赖一个名为 plasTeX 的 Python 库,它可以将 LaTeX 文档的源文件解析成一个 Python 对象树,而不是直接编译成 PDF。 - 识别特殊宏:在解析过程中,
leanblueprint会重点识别它自己定义的一套特殊 LaTeX 宏,连接文本与代码。 - 提取元数据:通过识别这些宏,
leanblueprint从.tex文件中提取出所有关键的元数据:所有数学声明的列表、它们对应的 Lean 名称、它们之间的依赖关系以及它们各自的形式化状态。 - 生成输出:利用提取出的元数据,
leanblueprint生成最终的输出:- 对于网页:它会生成 HTML 文件,并将元数据嵌入其中。例如,
\lean{MyMath.Group.assoc}会变成一个超链接,指向该 Lean 定义的 API 文档。\uses信息则被用来渲染那个强大的依赖图。 - 对于 PDF:它会忽略这些特殊宏,使用标准的
pdflatex将同一个.tex源文件编译成一篇格式优美的传统数学论文。
- 对于网页:它会生成 HTML 文件,并将元数据嵌入其中。例如,
这种架构设计具有显著的非侵入性特征:用户只需在 LaTeX 文档中添加少量特殊宏,就能获得完整的项目管理和现代化发布功能,无需改动任何 Lean 核心代码。
实战演示:构建数学形式化项目
我创建一个简单的代数结构项目,演示群论中的基本概念形式化过程。
项目初始化
首先,使用 Lean 的包管理器 lake 创建一个新项目。
1 | # 创建新的 Lean 项目 |
在 lakefile.lean 中添加必要的依赖,包括:
mathlib4:Lean 的标准数学库checkdecls:声明检查工具doc-gen4:文档生成工具
1 | require mathlib4 from git "https://github.com/leanprover-community/mathlib4" @ s!"v{Lean.versionString}" |
编写代码
修改入口文件 MyMathProject.lean:
1 | import MyMathProject.Basic |
创建文件 MyMathProject/Basic.lean,定义群的基本结构和性质:
1 | import Mathlib.Algebra.Group.Defs |
项目构建
完成代码编写后,我们需要构建项目并初始化 Blueprint 环境。
- 编译 Lean 项目:
1 | lake update |
- 由于 Blueprint 需要在 Git 版本控制下运行,我们需要初始化仓库并提交代码:
1 | # 复用 FLT 项目的 .gitignore |
Blueprint 配置
使用 Blueprint 的命令行工具创建项目模板:
1 | leanblueprint new |
在配置过程中,系统会询问一系列设置选项,按回车选择默认。由于我们已经手动配置了依赖,涉及 Modify lakefile and lake-manifest 的选项可以按 n 跳过。最终确认提交更改:
1 | ❯ leanblueprint new |
执行完成后,Blueprint 会生成以下目录结构:
1 | blueprint/ |
此外,因为配置了 doc-gen4,也附带构建了一个 home_page 目录用于项目主页。接下去是对 LaTeX 模板的修改,参考地址:Lean-zh/mathdemo.blueprint
Blueprint 提供了几个关键的 LaTeX 宏命令,用于关联数学文本和形式化代码:
\lean{...}:关联数学概念与 Lean 定义\uses{...}:声明定理间的依赖关系\leanok:标记已完成形式化的内容
构建与部署
生成文档和网站:
1 | leanblueprint all # 生成所有输出 |
对于 GitHub 部署,Blueprint 提供了自动化配置。只需在仓库设置中启用 GitHub Actions:
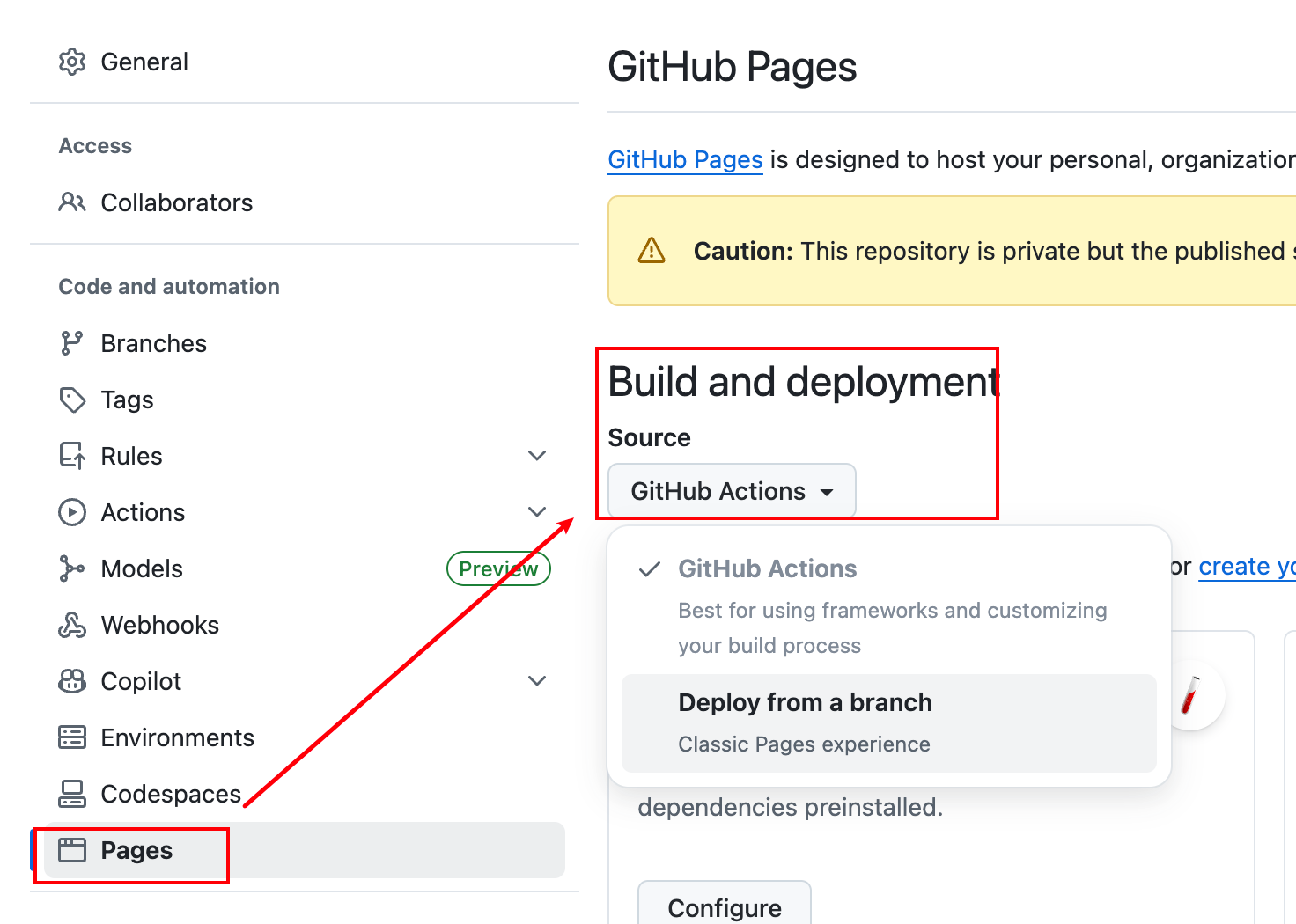
以上。
随着数学研究日益依赖计算机辅助证明,Blueprint 这类工具正在重塑数学研究的工作流程。它不仅是一个文档生成工具,更是连接传统数学写作和现代形式化方法的桥梁,为数学研究的未来开辟新的可能性。